§7.7将地面观测的长度归算到椭球面
根据测边使用仪器的不同,地面长度的归算可分为两种:一是基线尺量距的归算;二是电磁波测距的归算,现分别进行研究。
7.7.1基线尺量距的归算
将基线尺测量求得的长度加入尺段倾斜改正后,可认为它是基线平均水准面上的长度值,用![]() 表示。而我们所求的是椭球面上的大地线的长度s,因此产生了长度归算问题。
表示。而我们所求的是椭球面上的大地线的长度s,因此产生了长度归算问题。
1. 垂线偏差对长度归算的影响
由于垂线偏差的存在,使得垂线和法线不一致,水准面不平行于椭球面。为此在长度归算中应首先消除这种影响。假设垂线偏差沿基线是线性变化的,则垂线偏差u对长度归算的影响式是:
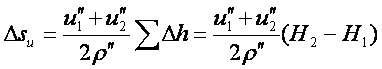 (7-97)
(7-97)
式中![]() 有关,其数值一般比较小,此项改正是否需要应结合测区及计算精度要求的实际情况进行具体分析。
有关,其数值一般比较小,此项改正是否需要应结合测区及计算精度要求的实际情况进行具体分析。
2. 高程对长度归算的影响
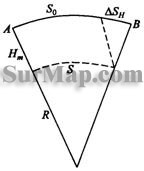 假设基线两端点已经过垂线偏差改正,则基线平均水准面平行于椭球体面。此时由于水准面离开椭球体面一定距离,也引起长度归算的改正。
假设基线两端点已经过垂线偏差改正,则基线平均水准面平行于椭球体面。此时由于水准面离开椭球体面一定距离,也引起长度归算的改正。
AB为平均高程水准面上的基线长度,以![]() 表示,现要计算其在椭球面上的长度S,由图可知
表示,现要计算其在椭球面上的长度S,由图可知
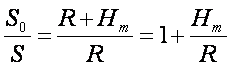
由此得椭球面上的长度为
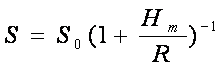 (7-98)
(7-98)
式中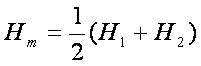 ,即基线端点平均大地高程;R为基线方向法截线曲率半径,按(7-55)式计算。
,即基线端点平均大地高程;R为基线方向法截线曲率半径,按(7-55)式计算。
如果将上式展开级数,取至二次项,则有
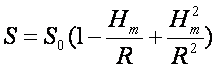 (7-99)
(7-99)
由此式可得由高程引起的基线归化改正数公式
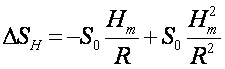 (7-100)
(7-100)
可见此项改正数主要与基线的平均高程![]() 及长度有关。
及长度有关。
顾及以上两式,则有地面基线长度归算到椭球面上长度的公式为:
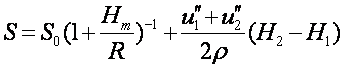 (7-101)
(7-101)
7.7.2电磁波测距的归算
![]() 间的大地线的长度S。
间的大地线的长度S。
我们知道:1) 在椭球面上两点间大地线长度与相应法截线长度之差是极微小的,故可忽略不计,这样可将两点间的法截线长度认为是该两点间的大地线长度;2) 两点间的法截线长度与半径等于其起始点曲率半径的圆弧长相差也很微小(如当S=640KM时,之差等于0.3米;S=200KM时,之差等于0.005m)。由于工程测量中边长一般为几公里,最长也不过十几公里,因而,这种差异又可忽略不计。因此所求的大地线长度可以认为是半径![]() 中,由余弦定理得:
中,由余弦定理得:
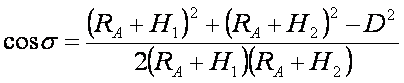
又 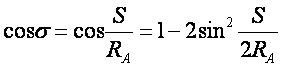
由以上两式得: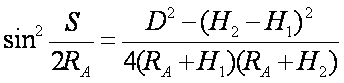
化简得:
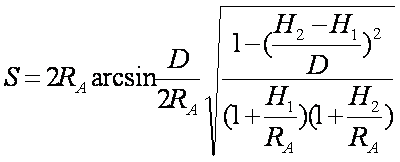 (7-102)
(7-102)
上式按反正弦函数展开级数并舍去五次项得:
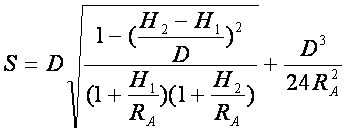 (7-103)
(7-103)
此式即为电磁波测距的归算公式。式中大地高H由两项组成:一是正常高,一是高程异常。为保证S的计算精度不低于![]() 达1公里即可。现对(7-103)式进一步简化如下
达1公里即可。现对(7-103)式进一步简化如下
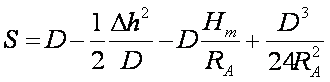 (7-104)
(7-104)
式中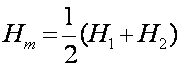 。显然,上式右端第二项是由于控制点之高差引起的倾斜改正的主项。经过此项改正,测线已变成平距;第三项是由于平均测线高出参考椭球面而引起的投影改正,经过此项改正后,测线已变为弦线;第四项则是由弦长改化为弧长的改正项。(7-103)式也可用下式表达:
。显然,上式右端第二项是由于控制点之高差引起的倾斜改正的主项。经过此项改正,测线已变成平距;第三项是由于平均测线高出参考椭球面而引起的投影改正,经过此项改正后,测线已变为弦线;第四项则是由弦长改化为弧长的改正项。(7-103)式也可用下式表达:
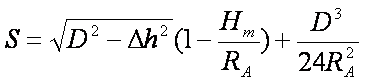 (7-105)
(7-105)
式中第一项显然是经高差改化后的平距。
将以上两式同(7-103)式相比较,我们便得两点间的弦长为,
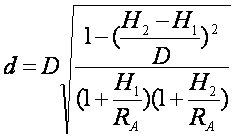 (7-106)
(7-106)
(此式在某些运算中有时用到)
经过以上各项改正的计算,即将地面上用电磁波测距仪测得的两点间的斜距化算到参考椭球面上。






