§8.7 距离改化公式
及其大地线S，
在高斯投影面上的投影为
两点的直线为D。
由S化至D所加的改正称为距离改正
。
计算公式。
8.7.1s与D的关系
设
弦上的微分线段，
因此 
由于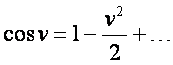
于是有
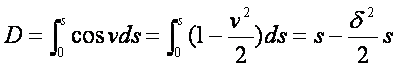(8-117)
式中
的最大值代替。
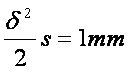，化算为相对中误差为
。所以，对现有测量方法这个误差可忽略不计，完全可以认为大地线的平面投影曲线长度s等于其弦线长度D。
8.7.2长度比和长度变形
长度比m是指椭球面上某一点的微分元素
之比，即
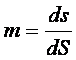
由于长度比恒大于1，故称
为长度变形。
1.用大地坐标表示的长度比公式
由（8-22）式第二式得
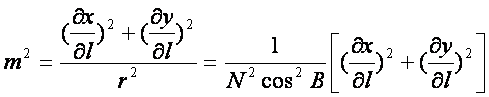(8-118)
偏导数见(8-78)
将上式代入(8-118)得
再根据近似公式
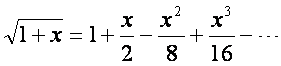
得
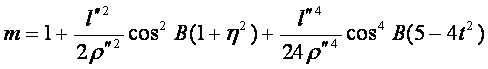(8-121)
实用时一般取至二次项
项。
2.用平面坐标表示的长度比公式
在(8-121)式中如果能将
用x,y表达，即可求得用平面坐标表示的长度比公式。利用正算公式(8-42)2式，
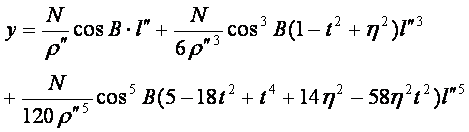(8-42)2
级数回求公式，若
则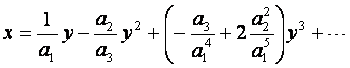 
这里
，
求得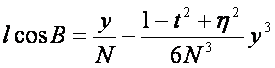 
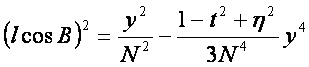（忽略六次项）
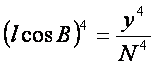（忽略六次项）
代入(8-121)式得
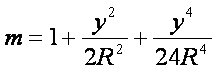(8-125)
分析(8-121)(8-125)式：
①m随点的位置(B,L)或(x,y)而异，但在一点上与方向无关；
②当y=0 (或l=0)时，即在纵坐标轴或中央子午线上时，各点的m都等于1，即中央子午线投影后长度不变；
③当
时，由于m是y（或l）的偶函数，且各项都为“+”号，故m恒大于1，即除中央子午线外其它投影后都变长了；
④长度变形（m-1）与
成正比例地增大，愈离远中央子午线长度变形愈大。
⑤在同一纬线上，即B=常数，长度变形（m-1）随l的增大而增大。
⑥在同一经线上，即l=常数，长度变形（m-1）随B的减少而增大，在赤道处(B=0)为最大。
8.7.3距离改化公式
长度比定义
由前面的分析知可用弦线来代替大地线的描写形，
积分之，
上式中长度比随点的位置而变，但当投影区域不大时，m的变化很缓慢，例如当y=300km，P1和P2两点的纬差达一度时，两点长度比之差小于4×10-7，因此用近似积分的方法而仍可得到较高的精度。现按辛普生近似积分公式，并且只把区间
分成两段，每段长s/2
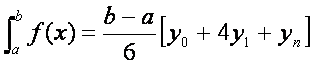
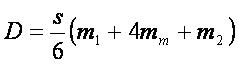
又按式(8-125)
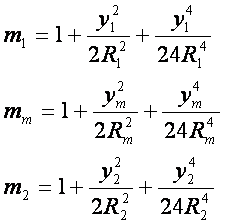
代入，并用
对计算影响可忽略不计，
又
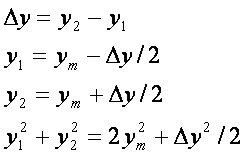
又因
项已是很微小，故完全可以作以下替换，
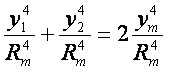
代入得大地线S归算到高斯平面上直线距离D的公式，
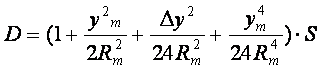（8-133）
当S<70km,
带的边缘) 计算精度小于0.001m，对于一
等边长的归算完全可满足要求，对于二等边长的归算可略去
项。
