高等级公路卵形曲线的计算方法

摘要　 在高等级公路施工过程中，常遇到卵形曲线，而设计单位的出发点不同，中线的解算方法也大相径庭。本文着重从卵形中线几种计算方法入手，在此基础之上阐述了卵形曲线的测设。
关键词　卵形曲线　复曲线　匝道桥　高等级公路
　　卵形曲线是高等级公路、立交桥匝道常见的曲线形式，它由基本的三部分构成：第一圆曲线段、缓和曲线段和第二圆曲线段。
　　中间段缓和曲线用来连接两个不同半径的圆曲线。其中线坐标解算方法有如下几种：
1 　补全缓和曲线
　　我国公路上采用的缓和曲线为辐射螺旋线，夹在两圆曲线中间的缓和曲线为整个缓和曲线的一部分，缓和曲线上任一点半径与该点至该缓和曲线起点的距离乘积为一定值： R×L ＝ A ，假设 R₁ ＞ R₂ ，可由两圆半径及两圆间的缓和段长 l_s ，求缓和曲线的总长 L 。

Δl ＝ L － l_s 　　 (1)

Δl 就是夹在两圆曲线间缓和段省去的部分，由 YH 点补长 Δl 至 o 点，以 o 点为该缓和曲线起点，起点的切线方向为 x 轴，与之垂直的曲线内侧方向为 y 轴方向建立坐标系（图 1 ）。缓和曲线公式（推导过程略）如下：

　　 (2)

　　 (3)

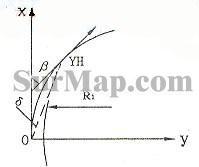
图　 1

　　利用 x 、 y 值可以求得 o—YH 弦与 x 轴的夹角： β ＝ 3δ 。 α₁ 为 YH 点的切线方位角，则 ox 的方位： α ＝ α₁±β 。 o 点的坐标可由几何关系求得为（ x₀ ， y₀ ）。缓和段上任一点统一坐标可求得：

　　 (4)

y=yo+xsinα±ycosα 　　 (5)

2 　曲率推算
　　缓和曲线段曲率半径由第一段圆曲线半径 R₁ 变为第二段曲率半径 R₂ （假设 R₁ ＞ R₂ ），则缓和曲线曲率半径变化为：

　　 (6)

其中 l_s 为中间段缓和曲线长，为求缓和曲线方程，现建立以缓和曲线起点为坐标原点，起点的切线方向为 x 轴，与之垂直的曲线内侧方向为 y 轴的坐标系（图 2 ），设 P 点为缓和曲线上任一点，距原点的曲线长为 l ，该点附近的微分弧长为 dl ，缓和曲线偏角为 β ，则有

dx=dlcosβ 　　 (7)

dy=dlsinβ 　　 (8)

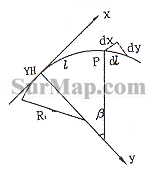
图　 2

由于

　　将其代入上式并进行积分可得缓和曲线方程：

　　 (9)

　　 (10)

　　中间缓和段统一坐标计算为：

　　 (11)

Y ＝ y_YHxsinα±ycosα 　　 (12)

　　 α 为曲线 YH 点切线方位。
3 　其它
　　连接两反曲线或在立交桥匝道上为使墩位美观，常采用缓和曲线连接（图 3 ）。其解算方法以 YH 点作为起点，以其切线为 x 轴建立坐标系，不考虑第一种情况中所讲的缓和曲线加长，而直接用式（ 2 ）、（ 3 ）进行计算，然后统一坐标。

图　 3

　　圆曲线坐标计算在此不再赘述。
　　全站仪广泛地应用到路桥施工中，外业施工放样可在仪器匹配的支持下自动完成。复曲线内业计算、复核线路坐标则成为繁琐问题。
4 　实例
　　已知 R₁ 为 5000m ， R₂ 为 90m ， YH 点切线方位 α₁ 为 327 － 56 － 59 ， YH 点里程为＋ 327 ． 9 ，坐标为（ 61205.283 ， 101834.119 ）， HY 点里程为＋ 416.28 ，坐标为：（ 61140.068 ， 101892.317 ）。
　　由已知数据可得：

　　
　　由式（ 2 ）、（ 3 ）计算填至附表第 3 、 4 栏内，由式（ 4 ）、（ 5 ）公式计算填入第 5 、 6 栏内。

作者简介：周烨，男， 1996 年毕业于辽宁工程技术大学测量工程专业，现任铁道部十九局二处助理工程师，先后参加过太峪隧道、南京长江二桥、宁台温高速公路等工程的施工建设。