间接平差又称参数平差。水平控制网按间接平差时,通常选取待定点的坐标平差值作为未知数(按方向平差时,还增加测站定向角未知数),平差后直接求得各待定点的坐标平差值,故这种以待定点坐标作为未知数的间接平差法也称为坐标平差法。参加平差的量可以是网中的直接观测量,例如方向、边长等;也可以是直接观测量的函数,例如角度等。由于三角网的水平角一般是采用方向观测法观测,并由相邻方向相减而得,故它们是相关观测值。此时,若不顾及函数间的相关性,平差结果将受到一定的曲解。因此,坐标平差法都按方向平差。
间接平差的函数模型是误差方程,它是表达观测量与未知数之间关系的方程式。一般工程测量平面控制网的观测对象主要是方向(或角度)和相邻点间的距离(即边长)因此坐标平差时主要列立各观测方向及观测边长的误差方程式,再按照间接平差法的原理和步骤,由误差方程和观测值的权组成未知数法方程去解算待定点坐标平差值,并进行精度评定。
本章主要研究(测)方向网、测边网以及测边测角网的严密坐标平差。
水平控制网按坐标平差法进行平差时,为降低法方程的阶数以便于解算,定向角未知数可采用一定的法则予以消掉。由于误差方程式的组成简单且有规律,便于由程序实现全部计算,因此,在近代测量平差实践中,控制网按间接平差法得到了广泛的应用。平面控制网按坐标平差时,网中每一观测值都应列立一个误差方程式。
 为便于计算,通常总是将观测值改正数表示为对应待定点坐标近似值改正数的线性式。坐标平差的第一步是列组误差方程式。对于方向网而言,参与平差的观测值是未定向的方向,选定的未知数是待定点的纵、横坐标值。误差方程式就是方向观测值改正数表达为待定点纵横坐标值的函数式,可以通过坐标方位角来建立方向值与未知数之间的联系。
为便于计算,通常总是将观测值改正数表示为对应待定点坐标近似值改正数的线性式。坐标平差的第一步是列组误差方程式。对于方向网而言,参与平差的观测值是未定向的方向,选定的未知数是待定点的纵、横坐标值。误差方程式就是方向观测值改正数表达为待定点纵横坐标值的函数式,可以通过坐标方位角来建立方向值与未知数之间的联系。
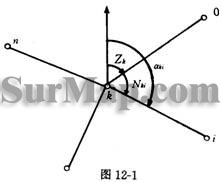
12.1.1方向误差方程式的建立和组成
在测站k上观测了![]() 等方向
等方向
其方向观测值为![]()
它们的改正数为![]()
![]() 的坐标方位角平差值方程为
的坐标方位角平差值方程为
![]() (12-1)
(12-1)
式中:![]() 方向的平差值,
方向的平差值,
![]() 方向的坐标方位角,通常称测站定向角,
方向的坐标方位角,通常称测站定向角,
![]() 的近似值,
的近似值,
![]() 的改正数,是个未知参数,
的改正数,是个未知参数,
![]()
如果令![]() ,
,
其相应的改正数分别为![]() ,
,
则有关系:
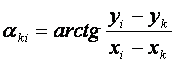 (12-3)
(12-3)
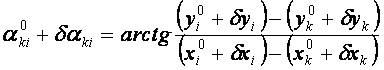
将上式按台劳级数展开,
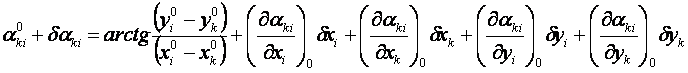
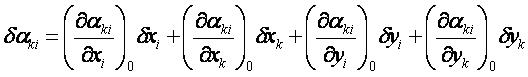
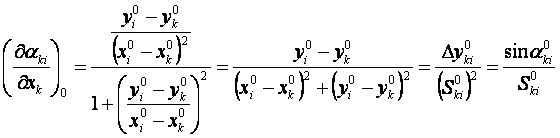
坐标方位角改正数方程:
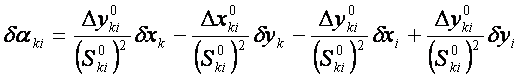 (12-5)
(12-5)
将(12-5)代入(12-4)然后再代入(12-1)得:
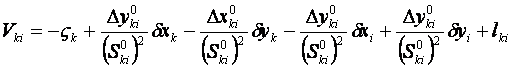 (12-6)
(12-6)
式中,
![]() (12-7)
(12-7)
计算中,![]() 以dm为单位,且换以
以dm为单位,且换以
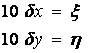
(12-6)变为,
![]() (12-8)
(12-8)
式中,
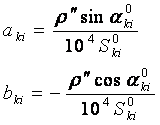 (10-9)
(10-9)
(12-6)和(12-8)式为方向误差方程式,考虑到边长误差方程式(12-35)式以便于编程常用(12-8)式。一般取第一方向的近似坐标方位角为定向角的近似值,即![]() ,这样,
,这样,
![]() (12-7)1
(12-7)1
(12-8)为一般式,
①当k为固定点,i为待定点时,![]() ,则误差方程式为:
,则误差方程式为:
![]() (12-12)
(12-12)
②当i为固定点,k为待定点时,![]() ,则误差方程式为,
,则误差方程式为,
![]() (12-13)
(12-13)
③当k,i都为固定点时,![]() ,则误差方程式为,
,则误差方程式为,
![]() (12-14)
(12-14)
④k,i对向观测时,由于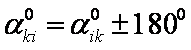 ,所以
,所以
![]() ,
,
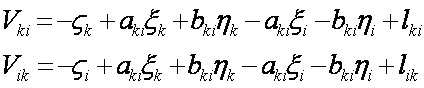 (12-15)
(12-15)
只有定向角未知数和常数项不同,其它全相同。
12.1.2误差方程式的改化---史赖伯法则
按方向坐标平差时,方向误差方程式有两个显著的特点:①是由同一测站上各观测方向所组成的误差方程式中,有共同的定向角未知数,且系数均为-1;②是对向观测的两个方向误差方程式同名未知数的系数相同。根据这两个特点,可对误差方程式进行改化(约化),以减少未知数(法方程式的阶数同样得到减少)和误差方程式的数目。由于这个方法是由史赖伯首先提出的,故称史赖伯法则,史赖伯法则共有三个法则。
1.消去定向角未知数法则
测站i有n个等权方向误差方程式
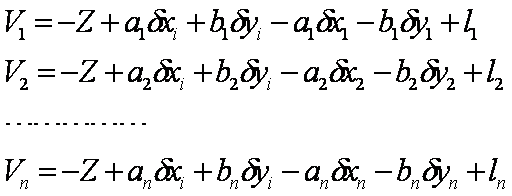
按定向角未知数向量![]() 进行分块,
进行分块,
 ,权P=E
,权P=E
显然![]()
组成法方程式
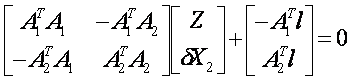
上式经约化而消去定向角未知数Z后,得约化方程
![]() (A)
(A)
史赖伯约化(改化)第一法则采用如下的虚拟误差式,
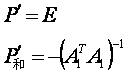 (B)
(B)
由(B)组成法方程式结果与(A)式完全相同。展开(B)2式
![]()
权 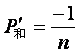
根据此法则,利用每测站加一个虚拟和方程式来消除该站的定向角未知数。
2.系数相同的误差方程式合并法则
设有n个未知数系数完全相同,但常数项和权不同的误差方程式,
![]() (12-26)
(12-26)
这n个误差方程式可用下面一个误差方程式代替,
![]() (12-27)
(12-27)
3. 误差方程式权的变换法则
设误差方程式,
![]() 权 P
权 P
可利用一个误差方程式代替,
![]()
当![]() 时,则
时,则
![]() 权1
权1
以上三式是等价的。
史赖伯法则,电算时一般只用到第一法则,手算时三个法则都可能用到。应用史赖伯法则时尚须强调三点,P172。
12.1.3三角网坐标平差的精度评定
1单位权中误差
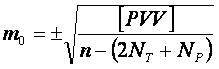 (12-28)
(12-28)
n观测方向总数;
![]() 待定点个数;
待定点个数;
![]() 设站(作方向观测)点的个数。
设站(作方向观测)点的个数。
一般平差时设各观测方向的权为1,则![]() 就是方向观测值的中误差。
就是方向观测值的中误差。
2.点位误差
坐标平差时协因数阵![]() 为第i个未知数的权倒数,
为第i个未知数的权倒数,
![]()
![]() (12-29)
(12-29)
![]()
还可求出待定点的误差椭圆元素和两待定点间的相对误差椭圆元素。
3.坐标未知数函数的精度
①边长![]() 的权函数式,
的权函数式,
![]() (12-30)
(12-30)
与边长的误差方程式(12-35)的差别只是没有常数项。
②坐标方位角![]() 的权函数式,
的权函数式,
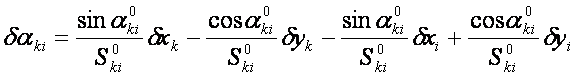 (12-31)
(12-31)
与方向误差方程式的差别只是没有常数项。
设每个权函数式的矩阵形式,
![]()
则它的协因数(权倒数),
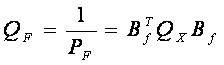
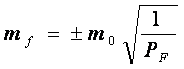 (12-33)
(12-33)
(12-34)式可不用,因用相对误差椭圆元素可求出任意两待定点之间的点位误差。






