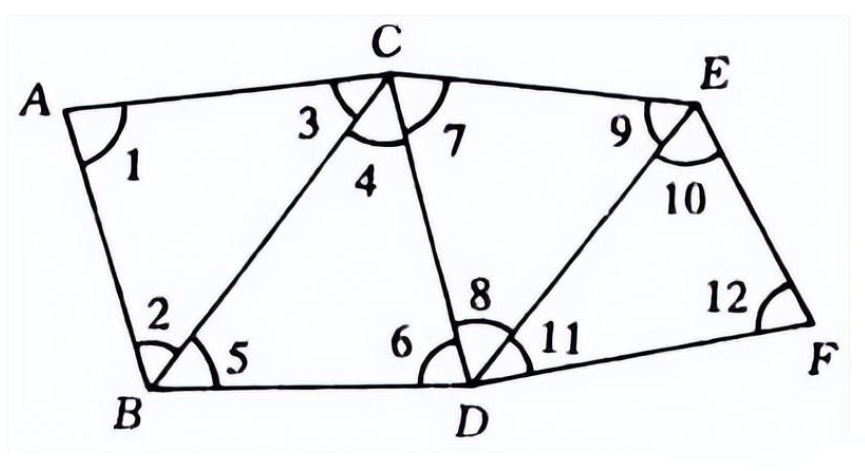
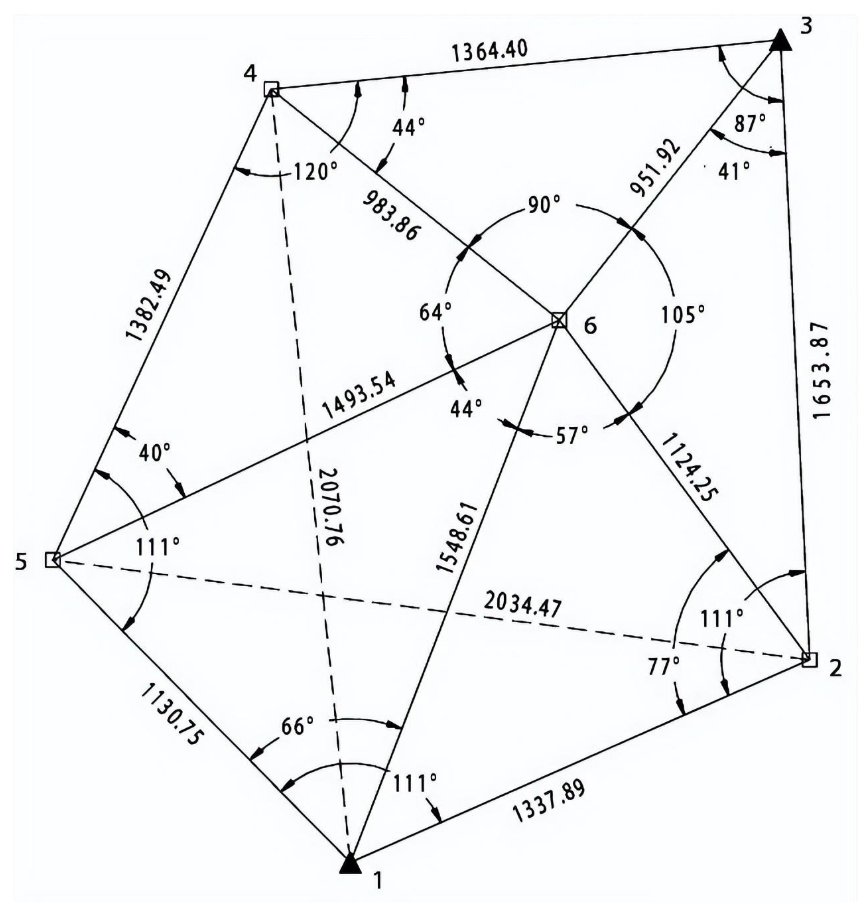
三角测量 在地面选一系列控制点,相互连接成若干个三角形,构成各种网(锁)状图形。先观测三角形的内角,再根据已知控制点的坐标、起始边的边长和坐标方位角,推算得到各三角形顶点水平位置的方法。它是几何大地测量学中建立国家大地网和工程测量控制网的基本方法之一,由荷兰的斯涅耳(W.snell)于1617年首创。20世纪50年代以前,国家大地网以及工程测量和城市测量中精密控制网的建立,几乎一律采用三角测量法。 三角测量作业分选定点位、造标埋石、水平角观测、成果计算等。点位一般应选在展望杰出、易于扩展的有利位置,使构成三角形的相邻点间互相通视。在选定的点位上建造觇标,供观测照准和升高仪器,同时埋设标石作为三角点的永久性标志。标石中心点是三角点的实际点位。水平角观测是三角测量的要害性工作,观测选在通视杰出、目标清晰稳定的有利时间进行。 三边测量 是在地面上布设一系列连续的三角形,采取测定各三角形的边长,按三角学原理推算各三角形的内角,从而计算出各边方位角和各三角点坐标的方法。是建立大地控制网和工程测量控制网的方法之一。与三角测量基本相同,但不观测水平角,而是利用电磁波测距仪或激光测距仪直接测定各三角形的边长。由于在地面上直接丈量距离一般困难很多,三边测量要求丈量所有的边,困难尤甚。直到1948年和1956年先后出现光电测距仪和微波测距仪后,三边测量法才得到实际应用。三边测量方法简捷,省工省时,在水平形变观测中应用较广泛。 由于用三边测量方法布设锁网不进行角度测量,推算方位角的误差易于累积,因此在网中需要有一定密度的已知方位边,以控制三边网的横向误差。矿区控制网一般是以国家大地网为基础建立,网中一般有一定数量的已知方位边,如密度不够则需测设起始方位边。 导线测量 将控制点用直线连接起来形成折线,称为导线;导线中的控制点称为导线点;点之间的折线边称为导线边;相邻导线边之间的夹角称为转折角;与坐标方位角已知的导线边(定向边)相连接的转折角称为连接角。通过观测导线边的边长和转折角,根据起算数据经计算而获得导线点平面坐标的工作即为导线测量。 为建立国家大地网和某些城市测量和工程测量所实施的导线测量,称为精密导线测量。其等级和精度要求与三角测量相同。这些个等级以下的导线测量,分为全站仪导线测量、视距导线测量和视差导线测量,其精度、施用的仪器和测量方法各不相同。 传统的精密导线测量 用基线尺在地面上直接丈量每相邻两点间的距离。因为距离测量的精度高,导线中不存在尺度误差积累;而方位误差积累则比三角测量严重。因此,导线上每隔一定距离要测定天文经纬度和方位角。因为导线以单线扩展,无其他几何校核,故必须闭合成环,或布设在高级控制点之间。当测区较大时,则构成导线网。 在一般地区,因为地面不平,难于用基线尺直接丈量距离,故传统的精密导线测量不及三角测量优越。但在平坦的森林地区,为了实施三角测量,必须建造过高的测量觇标,又为了断根通视障碍,还要砍伐树木,这样将使作业进展迟缓,用费较大。若改用导线测量,沿道路、林区分界地带或河流推进,利用平坦地势丈量距离,则可降低觇标高度,减少匡助工作,到达较好的经济效果。