◆钢结构连接计算
一、连接件类别
不焊透的对接焊缝
二、计算公式
1.在通过焊缝形心的拉力,压力或剪力作用下的焊缝强度按下式计算:
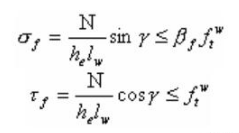
2.在其它力或各种综合力作用下,σf,τf共同作用处。
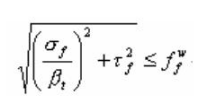
式中 N──-构件轴心拉力或轴心压力,取 N=100N;
lw──对接焊缝或角焊缝的计算长度,取lw=50mm;
γ─-作用力与焊缝方向的角度 γ=45度;
σf──按焊缝有效截面(helw)计算,垂直于焊缝长度方向的应力;
hf──较小焊脚尺寸,取 hf=30mm;
βt──正面角焊缝的强度设计值增大系数;取1;
τf──按焊缝有效截面计算,沿焊缝长度方向的剪应力;
Ffw──角焊缝的强度设计值。
α──斜角角焊缝两焊脚边的夹角或V形坡口角度;取 α=100度。
s ──坡口根部至焊缝表面的最短距离,取 s=12mm;
he──角焊缝的有效厚度,由于坡口类型为V形坡口,所以取 he=s=12.000mm.
三、计算结果
1. 正应力:
σf=N×sin(γ)/(lw×he)=100×sin(45)/(50×12.000)=0.118N/mm2;
2. 剪应力:
τf=N×cos(γ)/(lw×he)=100×cos(45)/(50×12.000)=0.118N/mm2;
3. 综合应力:
[(σf/βt)2+τf2]1/2=0.167N/mm2;
结论:计算得出的综合应力0.167N/mm2≤对接焊缝的强度设计值ftw=10.000N/mm2,满足要求!
◆钢结构强度稳定性计算
一、构件受力类别:
轴心受弯构件。
二、强度验算:
1、受弯的实腹构件,其抗弯强度可按下式计算:
Mx/γxWnx + My/γyWny ≤ f
式中 Mx,My──绕x轴和y轴的弯矩,分别取 100.800×106 N·mm,10.000×106 N·mm;
γx, γy──对x轴和y轴的截面塑性发展系数,分别取 1.2,1.3;
Wnx,Wny──对x轴和y轴的净截面抵抗矩,分别取 947000 mm3, 85900 mm3;
计算得:Mx/(γxWnx)+My/(γyWny)=100.800×106/(1.2×947000)+10.000×106/(1.3×85900)=178.251 N/mm2
受弯的实腹构件抗弯强度=178.251 N/mm2 ≤抗弯强度设计值f=215 N/mm2,满足要求!
2、受弯的实腹构件,其抗剪强度可按下式计算:
τmax = VS/Itw ≤ fv
式中 V──计算截面沿腹板平面作用的剪力,取 V=10.300×103 N;
S──计算剪力处以上毛截面对中和轴的面积矩,取 S= 947000 mm3;
I──毛截面惯性矩,取 I=189300000 mm4;
tw──腹板厚度,取 tw=8 mm;
计算得:τmax = VS/Itw =10.300×103×947000/(189300000×8)=6.441N/mm2
受弯的实腹构件抗剪强度τmax =6.441N/mm2≤抗剪强度设计值fv = 175 N/mm2,满足要求!
3、局部承压强度计算
τc = φF/twlz ≤ f
式中 φ──集中荷载增大系数,取 φ=3;
F──集中荷载,对动力荷载应考虑的动力系数,取 F=0kN;
tw──腹板厚度,取 tw=8 mm;
lz──集中荷载在腹板计算高度上边缘的假定分布长度,取 lz=100(mm);
计算得:τc = φF/twlz =3×0×103/(8×100)=0.000N/mm2
局部承压强度τc =0.000N/mm2≤承载力设计值f = 215 N/mm2,满足要求!
4、在最大刚度主平面内受弯的构件,其整体稳定性按下式计算:
Mx/φbWx ≤ f
式中 Mx──绕x轴的弯矩,取 100.8×106 N·mm;
φb──受弯构件的整体稳定性系数,取φb= 0.9;
Wx──对x轴的毛截面抵抗矩Wx,取 947000 mm3;
计算得:Mx/φbwx = 100.8×106/(0.9×947000)=118.268 N/mm2≤抗弯强度设计值f= 215 N/mm2,满足要求!
5、在两个主平面受弯的工字形截面构件,其整体稳定性按下式计算:
Mx/φbWx + My/γyWny ≤ f
式中 Mx,My──绕x轴和y轴的弯矩,分别取 100.8×106 N·mm,10×106 N·mm;
φb──受弯构件的整体稳定性系数,取φb= 0.9;
γy──对y轴的截面塑性发展系数,取 1.3;
Wx,Wy──对x轴和y轴的毛截面抵抗矩,分别取 947000 mm3, 85900 mm3;
Wny──对y轴的净截面抵抗矩,取 85900 mm3
计算得:Mx/φbwx +My/ γyWny = 100.8×106/(0.9×947000)+10×106/(1.3×85900)=207.818 N/mm2≤抗弯强度设计值f=215 N/mm2,满足要求!
◆钢筋支架计算公式
一、参数信息
钢筋支架(马凳)应用于高层建筑中的大体积混凝土基础底板或者一些大型设备基础和高厚混凝土板等的上下层钢筋之间。钢筋支架采用钢筋焊接制的支架来支承上层钢筋的重量,控制钢筋的标高和上部操作平台的全部施工荷载。型钢主要采用角钢和槽钢组成。
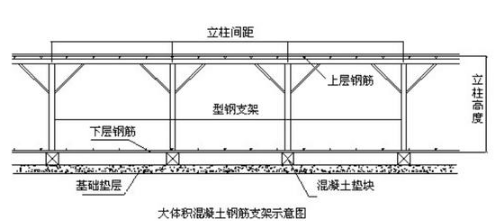
型钢支架一般按排布置,立柱和上层一般采用型钢,斜杆可采用钢筋和型钢,焊接成一片进行布置。对水平杆,进行强度和刚度验算,对立柱和斜杆,进行强度和稳定验算。
作用的荷载包括自重和施工荷载。
钢筋支架所承受的荷载包括上层钢筋的自重、施工人员及施工设备荷载。钢筋支架的材料根据上下层钢筋间距的大小以及荷载的大小来确定,可采用钢筋或者型钢。
上层钢筋的自重荷载标准值为0.800 kN/m;
施工设备荷载标准值为0.960 kN/m;
施工人员荷载标准值为1.248 kN/m;
横梁的截面抵抗矩W= 4.493 cm3;
横梁钢材的弹性模量E=2.05×105 N/mm2;
横梁的截面惯性矩I= 10.783 cm4;
立柱的高度h= 1.88 m;
立柱的间距l= 1.29 m;
钢材强度设计值f= 206.00 N/mm2;
二、支架横梁的计算
支架横梁按照三跨连续梁进行强度和挠度计算,支架横梁在小横杆的上面。
按照支架横梁上面的脚手板和活荷载作为均布荷载计算支架横梁的最大弯矩和变形。
1.均布荷载值计算
静荷载的计算值 q1=1.2×0.800+1.2×0.960=2.112 kN/m
活荷载的计算值 q2=q2=1.4×1.248=1.747kN/m
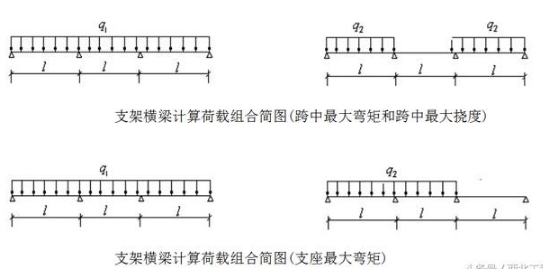
2.强度计算
最大弯矩考虑为三跨连续梁均布荷载作用下的弯矩
M1max=0.08q1l2+0.10q2l2
跨中最大弯矩为
M1=(0.08×2.112+0.10×1.747)×1.292=0.572kN.m
支座最大弯矩计算公式如下:
M2max=-0.10q1l2-0.117q2l2
支座最大弯矩为
M2=-(0.10×2.112 +0.117×1.747)×1.292=-0.692kN.m
我们选择支座弯矩和跨中弯矩的最大值进行强度验算:
σ=0.692×106/(4.493×103)=153.938N/mm2
支架横梁的计算强度小于206.00 N/mm2,满足要求!
3.挠度计算
最大挠度考虑为三跨连续梁均布荷载作用下的挠度
计算公式如下:
νmax=(0.677q1+0.990q2)l4/100EI
静荷载标准值q1= 0.800+0.960=1.760kN/m
活荷载标准值q2=1.248kN/m
三跨连续梁均布荷载作用下的最大挠度
Vmax=(0.677×1.760 +0.990×1.248)×12904/(100×2.05×105×10.783×104)=3.040mm
支架横梁的最大挠度3.040mm小于min(1290/150,10)mm,满足要求!
三、支架立柱的计算
支架立柱的截面积A=5.333 cm2
截面回转半径i=1.719 cm
立柱的截面抵抗矩W=6.062 cm3
支架立柱作为轴心受压构件进行稳定验算,计算长度按上下层钢筋间距确定:
σ = N/φA+Mw/W ≤ [f]
式中 σ──立柱的压应力;
N──轴向压力设计值;
φ──轴心受压杆件稳定系数,根据立杆的长细比λ=h/i,经过查表得到,φ=0.521;
A──立杆的截面面积,A=5.333 cm2;
[f]──立杆的抗压强度设计值,[f]=206 N/mm2;
采用第二步的荷载组合计算方法,可得到支架立柱对支架横梁的最大支座反力为
Nmax=0.617q1l+0.583q2l
经计算得到 N=0.617×2.112×1.290+0.583×1.747×1.290=2.995kN;
σ=2.995×1000/(0.521×5.333×100)+0.692×1000/6.062=124.878N/mm2;
立杆的稳定性验算 σ<[f],满足要求!
◆格构柱计算
格构柱肢体采用双肢柱,格构柱的计算长度lox= 1.00 m,loy= 1.00 m。
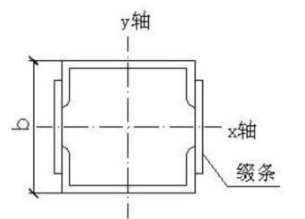
(1)y轴的整体稳定验算
轴心受压构件的稳定性按下式验算:
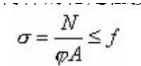
型钢采用双肢 5号槽钢,A=13.86 cm2, iy=1.10 cm;
λy=loy / iy=1.00×102 / 1.10=90.909 ;
λy≤[λ]=150,长细比设置满足要求;
查得φy= 0.615;
σ=50.00×103/(0.615×13.86 ×102)= 58.693 N/mm ;
格构柱y轴稳定性验算σ= 58.693 N/mm≤钢材抗压强度设计值 215 N/mm,满足要求;
(2)x轴的整体稳定验算
x轴为虚轴,对于虚轴,长细比取换算长细比。换算长细比λox按下式计算:
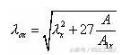
单个槽钢的截面数据:
zo=1.35 cm,I1 = 26 cm4,Ao=6.93 cm2;
整个截面对x轴的数据:
Ix=2×(26+ 6.93×(1.6/2- 1.35)2)= 56.193 cm4;
ix= (56.193 /13.86)1/2= 2.014 cm;
λx=lox / ix=1×102 / 2.014=49.664 ;
λox=[49.6642+(27×13.86 / 0.5)]1/2=56.701 ;
λox≤[λ]=150,长细比设置满足要求;
查得φx= 0.824;
σ=50×103/(0.824×13.860 ×102)= 43.754 N/mm ;
格构柱x轴稳定性验算σ= 43.754 N/mm≤钢材抗压强度设计值 215 N/mm,满足要求;






