准确的考虑建筑上部结构、基础与地基三者的共同作用是工程师们在进行地基基础和沉降控制设计时追求的终极目标。目前上部结构、基础的刚度的共同作用很多软件已经可以比较准确的考虑,但地基的刚度确定是个难点。这是必然的,结构上部和基础是人工建造组合成的一个三维的空间构架,现代的计算机已很容易用结构力学及有限元的方法来解答,但地基是宇宙几十亿年自然形成的,无论其力与变形的本构关系,还是土体本身的离散性,都使得土体的真实特性难以准确得到,这个问题也许永远不能如我们希望的那样完美的解决。
很多科研人员和结构工程师做了大量的实验和实际工程的总结得出了宝贵的经验。但不同的结构、基础形式,尤其是复杂的地基,再多的实验和实际也无法囊括一切。
因此结构工程师正确理解三者共同作用的概念或着说方向尤其重要。
如果要概念上清晰,我觉的在头脑里做几个思维实验是一个很好的方法,就像伽利略通过思维实验得出了没有外力作用的物体会无休止的匀速直线运动下去的结论。
一:思维模型的建立
下图是一个结构三者共同作用的思维实验的模型:

1:上部结构的刚度可以从0到∞。比如屋顶为铰接桁架的单层工业厂房的上部刚度几乎为0,而高层的剪力墙塔楼的刚度可以假定为∞。
2:基础的刚度可以为零,比如独立基础即基础之间互不关联刚度即为0,基础的刚度无穷大比如设备的块体基础。
3:地基的刚度可以设想很小~∞,不用设想刚度为零的情况,那样结构就悬空了。可以设想刚度很小的情况比如淤泥,这已经是结构的极限了。地基没有任何变形的情况下即为∞,比如花岗岩。
构思这个模型后,我们就可以随意设想三者共同作用下各部分不同刚度时地基反力的分布情况,也许有些设想的地基反力分布也许不一定对,这样就可以在有关的资料、实验数据和同行们的指导下修正自己的设想。得出了反力的分布就可以根据地基反力分布就可以大致判断出基础的内力和沉降了。
二:第一种思维模型;上部结构刚度的影响
1:假定基础和地基刚度不变时(均为有限刚),若上部刚度为零,这样上部结构即对基础只为外部荷载。这也是很多简化设计的计算方法。
见下图:
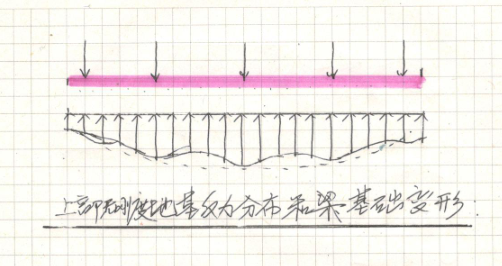
我们有土力学基本概念的工程师都可以基本思维出这个变形大致的形状,这个变形也即基础梁的挠曲线。
这个变形分两部分,一是整体弯曲挠度,二是局部弯曲挠度。
2:同样的地基和基础若上部刚度为无穷大时,地基反力分布如下图:

上图看出,因为上部结构为刚体,各柱底基础处沉降相同(不讨论刚体倾斜的情况),整体弯曲已经不存在了,只存在局部弯曲。
清华大学李广信老师土力学教材的图形比我手绘的更形象和准确,见下图:
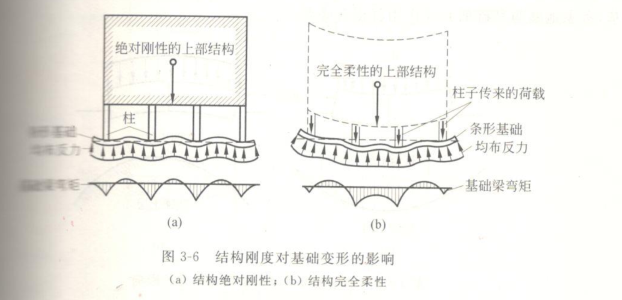
讨论:
(1)上述两种反力分布的图形的阴影面积是相同的,为上部结构的荷载之合。无刚度时整体结构整体弯曲中部变形大,刚度无穷大时,无整体弯曲,但局部弯曲度应该基本相同,见下图:

注:本图来源于李广信老师的基础工程教材。
方法1上部无限刚;2为上部刚度为零,3为上部有限刚。
图中可以看出,不同上部刚度的基础,局部弯曲的程度相差不大(和基础本身的刚度关系较大)。
地基反力、基础的变形和弯矩形状差不多,可以看出上部结构刚度越大,基础的内力(整体弯曲形成的弯矩和拉力)、结构的沉降越小。
(2)当上部结构刚度很大时,可以用倒楼盖来计算基础的内力。因为实际的地基反力是波浪形的,而倒楼盖的反力是直线,故倒楼盖算出的内力配筋偏于安全,这个要清楚。
(3)地基刚度一定时,上部结构及基础的总刚度越大地基反力分布越均匀,结构沉降和沉降差越小。
三:第二种思维模型,基础刚度的影响
当基础刚度无穷大时(此时上部结构的刚度大小失去了意义,无论其大小对地基的表现均为地基刚度无穷大),地基反力分布如下图:
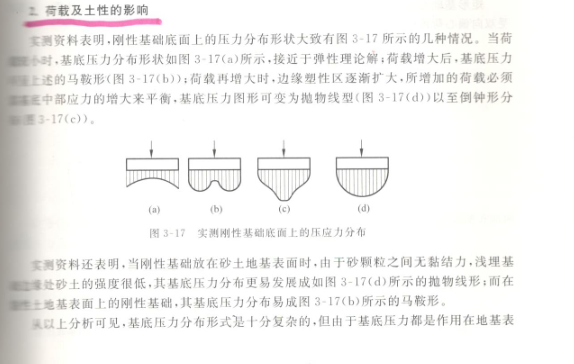

上述这段内容,其实是挺深奥的,我试着解读一下:
1、根据布辛内斯克解答,对于一个方形的柔性荷载(比如装满松散的砂土的无底方木箱),中点处地基除其上部的垂直投影的荷载外,受到四周的荷载的影响最大,故中点的沉降最大(见柔性荷载的沉降分布,注意和温克尔假定的区别)。但对于刚体基础来说,沉降是相等的,所以只有边缘受到的荷载大于中部时才有可能(如上图),而提供这种可能的条件是基础的不变形强制地基也不变形,因此基础会产生内应力。
2:为什么会出现c、d那样的图形呢?这其实是非常复杂的问题。
还得从布辛内斯克解讲。地基表面的荷载会在地基内部任一点产生三个方向即垂直方向和两个水平方向的应力,而两个水平方向的应力即为土体的剪力。因为土体在水平方向是连续的,所以水平方向不存在剪切破坏的问题,但沿着斜向即圆弧滑向地面的方向成了最弱的滑动面了。教材上说的边缘土体进入塑性状态本质上是土体的斜向地面的土体的剪切破坏导致边缘处的竖向承载力的降低,从而使应力分布从边缘向中部集中。理解斜向圆弧滑动面的原理,也就知道了地基深度修正的道理了,以及上图中的浅基础砂土强度底的道理了。
3:因为土体的互相影响,圣维南原理才可能正确。所以一定深度的土体的应力和表面土体应力的分布关系不大( 但对基础的内力的影响相对于对沉降的影响来说较大),所以规范的不考虑基底应力分布(只考虑荷载形状和总荷载)的计算地基沉降误差不大,误差大的是我们不知道现场地基土体的本构关系及土的离散状态。
4:上部刚度无穷大而基础刚度有限时和基础刚度无穷大时的地基分布有所区别。前者是像海平面一样,是大水平小波浪的形状,后者就是直线分布。倒楼盖的假定是直线分布,既然计算基础的内力那基础就是有限刚(比如刚体的高炉基础一般不计算内力,构造配筋即可),所以倒楼盖首先要求上部刚度很大,做到这一点,倒楼盖的直线分布对基础的内力就偏于保守了。
当上部结构刚度非常大时,可以不必按规范要求地基梁刚度的1/6限制,因为倒楼盖计算是保守的,只要基础梁计算符合规范受力要求即可。
规范规定的倒楼盖边跨反力增加20%的道理上图已经给出了原因。
另外需要明确的上述的讨论均为荷载合力作用点与基础形心重合时没有考虑整体的倾斜的情况。
四:第三种思维模型,地基刚度的影响
1、当上部结构刚度一定时(有限上部结构刚度)当地基无限刚时,地基反力分布见下图
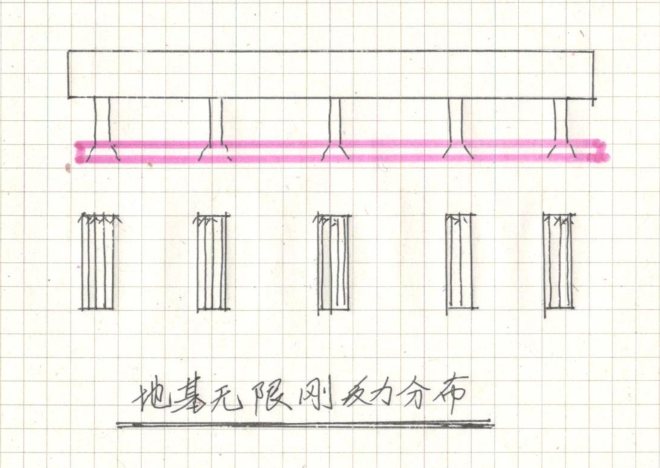
因地基无变形,上部结构轴力在基础内部45度扩散后(严格讲无变形时是不扩散的)直接传到同面积的部位,基础内力为零。
所以岩石地基可以不做基础,结构柱直接锚固地基里即可。
对于刚度比较大的地基,因反力集中,基础内力很小,可以不做连续基础,独立基础即可,道理就在这里。
对于桩筏基础,首先要求桩尽量布置在柱、墙的的下部,如果桩刚度很大,沉降变形小,中间的部位的筏板受力很小(相应的地基受力也很小),这时的应力分布类似上图的地基无限刚的形状。
复合地基反其道而行之,是加上褥垫层有意加大沉降来调节桩土返单的比列。复合桩基(无褥垫)考虑部分土的作用都是和沉降有关系。天然地基靠本来的刚度来使地基反力分布不同,而人工地基是人为的来调整刚度。人工地基的调平的优势就在这里,体现了人的能动性(当然需要化银子)。人工地基是非常复杂和有难度的一块,后续的文章试着思考总结一下。
2、若地基刚度很小时,上部结构刚度一般,地基反力见下图:
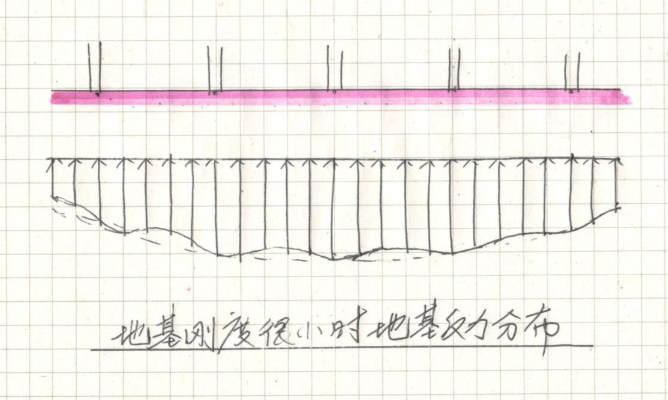
3、若上部结构刚度无穷大时,地基刚度很小时,地基的反力分布接近上文的这个图:
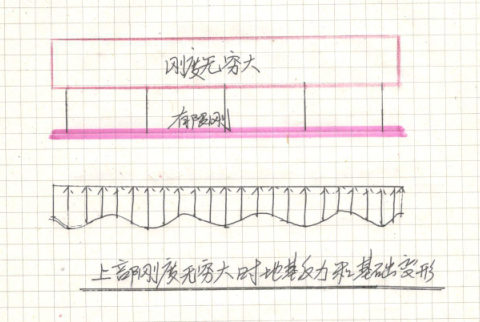
地基刚度越小,波峰越小,很小时几乎接近直线,但永远也不可能是直线。我们设想下地基刚度为零,也就是说地基变形无限大,成了自由落体了,地基反力为零,自然成直线了。
讨论:
(1)上部结构刚度一定时,地基刚度越大,地基反力的越向柱根部集中,反力分布越不均匀,但这是因为是地基沉降变形很小造成的。即地基越刚,地基变形越小,而地基反力越集中,这样基础内力会越小。
地基很刚是减少内力和沉降的根本原因,天然的好地基是建设方运气好,运气不好的时候人工加大地基的刚度比如复合地基或桩基就是很重要的手段了,但是需要花钱。
(2)当地基刚度一定时,上部结构刚度变化造成的地基反力的分布变化是不一样的。上部结构刚度越大,地基反力越平均,越平均地基的沉降和差异沉降就越小,基础的整体弯矩就越小,但局部弯矩并没有什么显著的变化。
上述的论述很绕,需要仔细体会。实际上述变化无需通过实际的实验和计算,有过基本结构和土力学知识的人仅仅通过思维大致方向可以想象出来。
(3)上部结构的刚度是建造上部结构时自然形成的,加大上部的刚度是上部结构本身的需要,而不是为了减少地基的沉降。目前上部结构设计时并没有考虑三者的共同作用,一般都是嵌固于基础进行设计即基础无限刚,所以在进行进行基础设计时,三者的共同中设计就会在上部结构产生上部结构设计时没有考虑到的额外的次应力,这个要做到心中有数。对于层数不高(一般高宽比小于4)的框架或框剪结构,要考虑次应力的不利影响。对于确实瘦高的建筑比如超高层、烟囱、高炉基础等,计算基础时上部的刚度不用就浪费了。
有些多层结构地基刚度比较勉强,而结构本身对沉降比较敏感,加大上部结构的刚度比如框架结构的拉梁、砖混结构的构造柱和圈梁等就是利用上部结构的刚度减少地基的不均匀沉降,其目的还是减少不均匀沉降对上部结构的影响。
(4)上部刚度一定时,地基刚度越小,整体变形越大,结构的不均匀沉降越大,这和我们的头脑概念是一致的。
(5)如果上部结构无限刚时,地基反力的分布和地基刚度有关,地基刚度越大,反力越向柱根集中,基础内力越小。
对于上部刚度足够大的情况,倒楼盖假定地基反力是直线分布所以是保守的设计方法。
(6)上部刚度不是很大的情况下,理论上倒楼盖法未必包的住,因为倒楼盖没有考虑整体弯曲,所以规范做了很多限制比如上部和基础的刚度,荷载的均匀等约束。实际上因为上部都有一定的刚度,而且基础整体弯曲的中和轴在结构上部,且基底的摩擦作用,实际的整体弯矩一般远远小于计算(有轴力),所以考虑局部弯曲的倒楼盖计算配筋和有通常配筋构造的基础实践证明是足够安全的。
五:温克尔假定和基床系数、地基土互相作用的布辛内斯克理论的再讨论
(1)地基土的互相作用是客观存在的, Winkler在那个晶体管计算机也没有的年代建立了温克尔地基模型的目的应该是为了基础内力的解析解能够实现(那时候还没有计算机的数值解法)。现代计算机已经可以用综合压缩模量来用互相作用的布辛内斯克理论进行求解了,所以温克尔假定应该淘汰了,教材中讲解应该只是为了学生了解地基设计的发展过程。
(2)我们上述的思维是自然的考虑了土体之间的互相作用(布辛内斯克J. Boussinesq 解),如果按温克尔假定,上述的思维全不对了,读者可以试着思考一下。
(3)地基综合模量的参数会改变地基反力的分布,但对基础的内力影响不大,不必过分担心参数的不准确会影响基础配筋的安全,所以在基础配筋计算时,模量可以估算,用规范分层综合的综合模量工程上是足够的。
下图是我假定的一个例题,不同基床系数时,基础梁弯矩变化。
基床系数10000到1000时,差10倍弯矩几乎不变,接近倒楼盖了。这个基床系数的变化即地基刚度的变化的影响和上述的思维实验相吻合。

(4)地基基础真正的难点是基础沉降的计算,模量的准确与否与沉降的大小关系极大,所以在沉降计算时应尽量使用符合实际情况的模量参数。
(5)基床系数仅用来计算配筋的,准确性要求不高。基床系数的获得无论现场实验或压缩模量的分层综合得到,都是先算出沉降在反算出来的。用温克尔的基床系数还是布辛解的综合模量,在基础配筋计算工程上误差可能不大(建议有人做个对比分析),但为了概念清楚还是布辛解合理,而且布辛解得出的筏板基础的沉降是合理的,当然沉降的计算对综合模量的准确性要求是很高的。
(6)既然地基反力的分布对基础内力影响不大,规范估算直接给出不同情况下地基反力的分布系数是个不错的方法(无需用模量和有限元的方法计算出所谓的准确的反力分布),比如高层筏基及箱基规范就是这样做的,建议这个工作更细致些,多列出一些不同情况的反力分布表。
地基沉降和基底表面的分布关系不大,就可以用总荷载和基础的形状来进行沉降的计算了。用有限元的计算方法算不同点的地基的沉降数据太细碎,和规范的限制作比较不可信,可能造成地基基础的浪费。
(7)输入模量参数按有限元的方法算出基础地面的地基反力分布和地基承载力去比较也是太细碎不可信,也可能造成地基基础的浪费。按规范简化计算的方法计算地基反力和地基承载力去比较是有大量的工程实践证明了的。






