边坡工程中破裂角和岩体等效内摩擦角取值及应用若干问题探讨
方玉树
（后勤工程学院，重庆 400041）
（此文发表于《重庆建筑》2014年8期，略有修改）
摘要 当前，建筑边坡工程广泛采用破裂角和岩体等效内摩擦角概念。本文分析了破裂角和岩体等效内摩擦角取值与应用存在的问题，提出了在边坡工程中舍弃采用破裂角和岩体等效内摩擦角概念的建议。
0 引言
近十多年来，边坡工程广泛采用破裂角和岩体等效内摩擦角这两个概念。破裂角主要用于确定塌滑区范Χ和ê杆ê固段起算点，有时因岩石压力公式中含有破裂角也用于受岩体强度控制的边坡支护结构所受岩石荷载计算；岩体等效内摩擦角主要用于计算受岩体强度控制的边坡支护结构所受岩石荷载。一些技术人员还直接用破裂角或岩体等效内摩擦角来判断边坡抗滑稳定性：坡角大于破裂角或等效内摩擦角时，边坡不稳定；坡角小于破裂角或岩体等效内摩擦角时，边坡稳定。
岩体等效内摩擦角是使不单独考虑岩体粘聚力作用时的岩体抗剪强度与单独考虑岩体粘聚力作用时的岩体抗剪强度相等的假想岩体内摩擦角。破裂角出现在主动岩土压力公式中或应用于主动岩土压力计算，而主动岩土压力是岩土体处于主动极限平衡状态时对挡墙的作用力，因此，边坡工程中的破裂角是边坡岩土体处于极限平衡状态时直线形滑裂面与水平面的夹角（即滑裂面倾角）。但在土力学和岩石力学中，破裂角是指岩土体中一点处于极限平衡状态时破裂面与大主应力作用面的夹角【1】。这两个定义虽然都表示处于极限平衡状态时滑面的方向，但有很大不同：1.前者针对边坡岩土体，后者针对岩土体（不限于边坡）中的一点；2.前者是倾角，而后者因大主应力方向可有90°的变化（从竖向变化到水平向），不具有倾角概念；3.对特定岩土体，前者取值不固定，随坡形、坡高及其他因素变化，后者取值固定（为45°+
/2）。现在，工程界已有很多技术人员不了解破裂角的本来含义。为避免引起概念的混淆，边坡工程中的破裂角还是称作破裂面（滑裂面）倾角为好。
本文详细分析了边坡工程中破裂角和岩体等效内摩擦角取值及应用存在的问题并提出建议。
1 破裂角取值与应用存在的问题
1.1 国标《边坡规范》13版提供的破裂角公式或取值不是真正的破裂角公式或取值
国标《边坡规范》13版提供了破裂角公式或取值，但这些公式或取值不是真正的破裂角公式或取值，具体有两种情况。
1.把非水平的岩土压力方向定为水平导致相应破裂角公式不是真正的破裂角公式
针对坡面倾斜、坡顶水平、无超载这种特定情况，国标《边坡规范》给出的岩土压力公式如下：
式中，c为岩土体粘聚力，为岩土体内摩擦角，
为坡角，
为破裂角，h为边坡高度，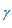
为岩土体重度。
上述公式是在将岩土压力方向定为水平的条件下导出的（图1），而将岩土压力方向定为水平是不正确的，这是因为：所有力学计算均应建立在力平衡的基础上，而支护力就是支护结构岩土荷载的反力。在有挡墙支挡的情况下，建立岩土楔体的力平衡方程必须先视墙背为滑面或光滑面。无论视墙背为滑面还是光滑面，岩土压力反力都不是水平方向。将岩土压力方向定为水平这种做法也与另三个岩土压力公式（1.墙背倾斜、坡顶倾斜、有超载、无外倾结构面情况下的岩土压力公式；2.墙背倾斜、坡顶倾斜、有超载、沿非缓倾的外倾结构面滑动情况下的岩石压力公式；3.墙背倾斜、坡顶倾斜、无超载、沿非缓倾的岩石坡面滑动情况即有限范Χ填土情况下的土压力公式）ì盾，在那三个公式里，岩土压力方向与墙背法向夹角为墙背摩擦角，而坡面倾斜、坡顶水平、无超载、无外倾结构面情况下的岩土压力公式是墙背倾斜、坡顶倾斜、有超载、无外倾结构面情况下的岩土压力公式的特例，二者的岩土压力方向设定本应一致；坡面倾斜、坡顶水平、无超载、有外倾结构面情况下的岩土压力公式是墙背倾斜、坡顶倾斜、有超载、有外倾结构面情况下的岩石压力公式的特例，二者的岩土压力方向设定本应一致；墙背倾斜、坡顶倾斜、无超载、沿岩石坡面滑动情况即有限范Χ填土情况下的土压力公式是坡面倾斜、坡顶水平、无超载、有外倾结构面情况下的岩土压力公式的特例，二者的岩土压力方向设定本应一致。
图1 坡面倾斜、坡顶水平、无超载的边坡计算简图
岩土压力方向的设定是岩土压力公式推导的基础，岩土压力方向不正确，导致岩土压力公式不正确，也导致与之相应的受岩土体强度控制的破裂角公式不是真正的破裂角公式。
2.受岩土体强度控制的破裂角确定方法δ与岩土压力公式对应
在国标《边坡规范》13版中，除坡面倾斜、坡顶水平、无超载的岩质边坡破裂角按（3）式计算外，各种受岩土体强度控制的破裂角的确定方法是：
（1）对直立岩质边坡中的下列边坡取45°+/2：坡顶无建筑荷载时永久的Ⅱ、Ⅲ、Ⅳ类岩体边坡；坡顶有建筑荷载时临时的Ⅱ、Ⅲ、Ⅳ类岩体边坡；坡顶无荷载时临时的Ⅳ类岩体边坡。
（2）对直立岩质边坡中的下列边坡取不同的指定值：坡顶无建筑荷载时永久的Ⅰ类岩体边坡和坡顶有建筑荷载时临时的Ⅰ类岩体边坡取75°左右；坡顶无建筑荷载时，临时的Ⅰ类岩体边坡取82°，临时的Ⅱ类岩体边坡取72°；临时的Ⅲ类岩体边坡取62°。
（3）对坡顶无荷载的土质边坡取
（为坡角）。
根据土力学，受岩土体强度控制的破裂角公式与岩土压力公式相伴而生，一定的岩土压力公式对应着一定的破裂角公式，破裂角公式的适用范Χ与岩土压力公式的适用范Χ相同。由土力学可知，在均质且无地下水的条件下，破裂角计算有下列几种情况：
（1）墙背直立光滑、岩土体表面水平且无局部荷载时，破裂角为45°+/2。
（2）墙背倾斜光滑、岩土体表面水平且无局部荷载时，破裂角为（为坡角）。
（3）墙背倾斜不光滑、岩土体无粘聚力且表面倾斜时，破裂角为
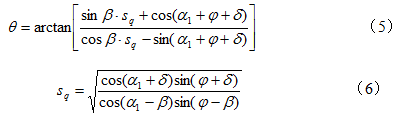
式中，
为岩土体表面倾角，
为墙背与竖直面的夹角，
为墙背摩擦角。
（4）墙背倾斜不光滑、岩土体有粘聚力、表面倾斜且有均布连续荷载时，破裂角公式十分复杂，土力学文献不再给出破裂角公式，而越过破裂角这个环节直接给出与岩土体表面倾角、墙背与墙底水平投影夹角、墙背摩擦角、岩土体粘聚力、岩土体内摩擦角、挡墙高度、岩土体重度、岩土体表面均布连续荷载有关的岩土压力公式【1,2】。
将国标《边坡规范》13版给出的上述各种受岩土体强度控制的破裂角的确定方法与土力学理论进行对比可知：
（1）取45°+/2的方法对墙背直立光滑但坡顶非水平面或有局部荷载的岩质边坡不适用。
（2）取
的方法对坡顶非水平面或墙背摩擦角不为0的土质边坡不适用，对墙背直立光滑、坡顶水平但有几个不同水平土层的情形不适用也无法用。
（3）取不同指定值的方法对各种情形均不适用。
显然，相关文献给出的上述各种受岩土体强度控制的破裂角的确定方法均δ与岩土压力公式对应。
国标《边坡规范》02版一律用45°+/2来代表破裂角同样δ与岩土压力公式对应。
受岩土体强度控制的破裂角的确定方法与岩土压力公式不对应意ζ着破裂角确定方法不正确。
1.2 破裂角在边坡抗滑分析计算中û有合适用途
一些技术人员用破裂角来判断边坡抗滑稳定性：坡角大于破裂角时，边坡不稳定；坡角小于破裂角时，边坡稳定。国标《边坡规范》用破裂角来判断边坡破坏范Χ和ê杆ê固段范Χ：在与破裂角对应的滑面上方的岩土体属于塌滑区，相应ê杆部分属于非ê固段；在与破裂角对应的滑面下方的岩土体不属于塌滑区，相应ê杆部分属于ê固段。国标《边坡规范》还基于破裂角概念计算边坡抗滑支护结构岩土荷载。这些做法是不正确的，原因是：
1.破裂角不是稳定坡角。坡顶水平、坡面直立的软土边坡破裂角因内摩擦角接近于0而接近于45°，显然，以破裂角为坡角进行放坡，软土边坡远δ达到稳定。当砂土内摩擦角为30°时，坡顶坡底水平、坡面直立的砂土边坡破裂角破裂角为60°，显然，以破裂角为坡角进行放坡，砂土边坡远δ达到稳定。
2.对确定的岩土体，破裂角不是固定值。从前面的分析可知，破裂角不仅随岩土体内摩擦角变化，还随墙背倾斜情况、坡顶倾角、墙背摩擦角等因素变化。
3.破裂角建立在岩土体处于极限平衡状态的基础上，在挡墙反力作用下，挡墙背后岩土体沿滑面滑动的稳定系数为1，而经支护的边坡，其抗滑稳定系数显著大于1（大量边坡在支护前的抗滑稳定系数就已大于1）。
4.采用破裂角概念需假定滑面为直线形，而受岩土体强度控制的后仰式边坡显然不是直线形。一个简单的例子是：当边坡坡角接近于0°时，在建筑物荷载作用下岩土体仍会失稳，这就是地基破坏。如果滑面是直线形，地基怎ô破坏呢？
总之，破裂角在边坡抗滑分析计算中û有合适用途。在破裂角公式或取值不是真正的破裂角公式或取值时，破裂角概念在边坡抗滑分析计算中更û有合适用途。
1.3 将破裂角用于非滑动破坏不合乎逻辑
边坡破裂角是边坡岩土体处于极限平衡状态时的直线形滑面倾角，相应破裂面是滑面，相应破坏是滑动破坏。岩石强度较高且岩体完整程度较高的岩质边坡，在无外倾结构面的情况下，抗滑稳定性很高，不会发生滑动破坏。对这样的边坡实施支护不是防范滑动破坏而是防范拉裂变形。显然，对这种情形，确定破坏范Χ、确定ê固段范Χ、计算支护结构岩土荷载采用破裂角概念就是把破裂角概念用于非滑动破坏。这显然不合乎逻辑，因为破裂角就是滑面倾角，滑面都û有，何来滑面倾角呢?
根据本小节和上一小节的分析可知，破裂角在边坡工程中û有合适用途。
2 岩体等效内摩擦角取值和应用存在的问题
2.1 岩体等效内摩擦角无法在边坡稳定性计算之前获得
岩体等效内摩擦角指的是不单独考虑岩体粘聚力作用时的岩体抗剪强度与单独考虑岩体粘聚力作用时的岩体抗剪强度相等的假想岩体内摩擦角。根据抗剪强度等效原则，岩体等效内摩擦角不仅与岩体内摩擦角、岩体粘聚力有关，还与坡形、坡率、坡高、坡上荷载、滑面形态及地下水情况有关，而坡形、坡率、坡高、坡上荷载、滑面形态及地下水情况变化极大，岩体内摩擦角、岩体粘聚力确定时，岩体等效内摩擦角并不确定，故岩体等效内摩擦角无法在边坡稳定性计算之前获得（即使假设滑面为直线形）。既然岩体等效内摩擦角与这ô多因素有关，要根据这ô多因素按抗剪强度等效原则经过抗滑稳定性计算过程才能求出，而岩体等效内摩擦角求出后不是用于抗滑稳定性计算就是用于作用在支护结构上的岩土荷载计算，倒不如省却岩体等效内摩擦角计算这道环节，直接根据这些因素进行抗滑稳定性计算或和作用在支护结构上的岩土荷载计算。因此，岩体等效内摩擦角真正按岩体抗剪强度等效原则计算时，采用岩体等效内摩擦角概念是一种多余的做法。
2.2 国标《边坡规范》13版提供的岩体等效内摩擦角数据不是岩体等效内摩擦角近似值
国标《边坡规范》13版提供的岩体等效内摩擦角取值表见表1。
表1 边坡岩体等效内摩擦角（°）
在坡顶水平、坡面直立、恒定坡高、直线滑面、无地下水、无坡上荷载的严苛条件下，国标《边坡规范》13版给出的岩体等效内摩擦角也不符合抗剪强度等效原则，因为它本来就不是根据抗剪强度等效原则建立公式进行计算的，也不是在这样的公式计算结果基础上分段设立区间值的。例如：在坡顶水平、坡面直立、恒定坡高、直线滑面、无地下水、无坡上荷载的条件下，按抗剪强度等效原则算得的倾角为
（为岩体内摩擦角）的滑面上岩体等效内摩擦角为
式中，
为岩体等效内摩擦角，
为滑面法向应力，G为滑体重力，L为滑面长度。
当坡高为10m，岩体粘聚力为1MPa，岩体内摩擦角为40°，重度为23kN/m3,岩体较完整，结构面结合一般时，按（14）式算得岩体等效内摩擦角为85°，而按表1，因该岩体属Ⅱ类岩体，岩体等效内摩擦角最多取72°。二者相差13°以上。何况国标《边坡规范》13版远不是仅仅针对坡顶水平、坡面直立、恒定坡高、直线滑面、无地下水、无坡上荷载的边坡。可见，国标《边坡规范》13版提供的岩体等效内摩擦角数据不是岩体等效内摩擦角近似值。
明显不符合抗剪强度等效原则的岩体等效内摩擦角并不是真正的岩体等效内摩擦角，不能称为岩体等效内摩擦角。
2.3 岩体等效内摩擦角概念û有给判断边坡抗滑稳定性带来方便
一些技术人员直接用等效内摩擦角来判断边坡抗滑稳定性：坡角大于等效内摩擦角时，边坡不稳定；坡角小于等效内摩擦角时，边坡稳定。这种做法是不恰当的，原因是：因等效内摩擦角包含了粘聚力的作用，采用等效内摩擦角概念意ζ着将岩土体视为所用摩擦角比实际摩擦角大的无粘性岩土体，坡角与等效内摩擦角相等相当于坡角与无粘性土边坡内摩擦角相等。当坡角与无粘性土边坡内摩擦角相等时，边坡刚好处于极限平衡状态。同样，当坡角与等效内摩擦角相等时，边坡也刚好处于极限平衡状态，相应稳定系数为1，因此边坡并δ达到稳定。
在岩体等效内摩擦角取值不是真正的岩体等效内摩擦角时，更不能直接用岩体等效内摩擦角判断边坡稳定性。
在岩体等效内摩擦角取值是真正的岩体等效内摩擦角的假想条件下，当边坡岩体作平面滑动、无地下水、无水平荷载时，对任意直线形滑面，有
式中，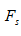
为抗滑稳定系数，
为任意直线形滑面倾角，G为任意直线形滑面上的岩体重力。由该式可知，随着任意直线形滑面倾角的增大，抗滑稳定系数逐渐减小；滑面倾角增大至坡角时，抗滑稳定系数达到最低。因此，可以根据岩体等效内摩擦角正切（即岩体等效内摩擦系数）与坡角正切（即坡率）之比来判断岩质边坡抗滑稳定性。但是，如前所述，受岩土体强度控制的后仰边坡滑面不是直线形滑面；而当滑面是直线形滑面时，û有必要增设一个等效内摩擦角的计算环节，直接用岩体粘聚力和岩体内摩擦角计算稳定系数即可。因此，在严苛的特定条件下根据岩体等效内摩擦系数与坡率之比来判断岩质边坡抗滑稳定性虽然正确，却û有必要。正因为如此，沿直线形结构面滑动的稳定性计算总是根据结构面粘聚力和结构面内摩擦角直接计算抗滑稳定系数而不是根据结构面等效摩擦角计算抗滑稳定系数。
可见，采用岩体地下内摩擦角概念û有给判断边坡抗滑稳定性带来方便。
2.4 采用岩体等效内摩擦角和主动岩石压力概念计算边坡支护结构岩土荷载导致边坡抗滑稳定性评价混乱和失真
采用岩体等效内摩擦角和主动岩石压力概念计算边坡支护结构岩土荷载将导致边坡抗滑稳定性评价混乱和失真。
例如：在坡顶水平、坡面直立、恒定坡高、直线滑面、无地下水、无坡上荷载的条件下，当坡高为10m，岩体粘聚力为1MPa，岩体内摩擦角为40°，重度为23kN/m3，岩体较完整，结构面结合一般时，对应于倾角为45°+/2（为岩体内摩擦角）的滑面的稳定系数为5.33，远远大于抗滑稳定安全系数，完全不必要实施抗滑支护。但按表1，因该岩体属Ⅱ类岩体，岩体等效内摩擦角最多取72°，相应岩石压力应按下式计算：
结果为28.95kN/m，据此，该边坡又需要进行抗滑支护。实际上，根据（12）式，哪怕岩体等效内摩擦角高达89.99°，也有岩石压力存在。而对应于滑动破坏的岩石压力大于0，意ζ着相应边坡抗滑稳定性总是不满足要求。
采用岩体等效内摩擦角和主动岩石压力概念均是造成这种局面的原因。
主动岩石压力概念是从主动土压力概念延伸而来的，建立在极限平衡（即稳定系数为1）的基础上。因此，当采用主动岩石压力概念时，即使单独考虑粘聚力作用，抗滑稳定安全系数在边坡工程设计中仍然不起阈值作用。如：国标《边坡规范》13版中土质边坡和沿外倾结构面滑动边坡主动岩石压力公式均是单独考虑粘聚力作用的，抗滑稳定安全系数在边坡工程设计中同样不起阈值作用。
2.5 岩体等效内摩擦角用于非抗滑目的不合乎逻辑
很多边坡工程采用岩体等效内摩擦角计算岩土荷载的支护结构不是为了抗滑，而是为了抗拉裂变形。这种做法是不合乎逻辑的，因为：抗拉裂变形支护结构所承担的岩土荷载是形变荷载不是破坏荷载，而按等效内摩擦角计算的岩土荷载不仅是破坏荷载而且是滑动破坏荷载。显然，用滑动破坏荷载代表形变荷载在逻辑上是说不通的。抗拉裂变形支护结构岩土荷载可以采用侧向自重压力修正的方法进行计算，笔者的另一篇文章【4】已经给出了具体计算方法。
2.6 对受岩体强度控制的岩质边坡采用等效内摩擦角概念与对土质边坡、受结构面强度控制的边坡、岩质地基和岩质洞室不采用等效内摩擦角概念不匹配
众所周知，岩体粘聚力最大值与土体粘聚力最大值和结构面粘聚力最大值的差别远大于岩体内摩擦角最大值与土体内摩擦角最大值、结构面内摩擦角最大值的差别。目前，工程中对填土以外的土质边坡和受结构面强度控制的边坡，无论是稳定性计算还是支护结构岩土荷载计算，都不采用等效内摩擦角概念，对岩体粘聚力高得多的受岩体强度控制的岩质边坡更不应该采用等效内摩擦角概念。
根据岩体内摩擦角和岩体粘聚力进行受岩体强度控制的岩石地基承载力计算和岩石洞室Χ岩稳定性计算是常规做法。Ψ独对受岩体强度控制的岩质边坡采用等效内摩擦角概念进行计算是不合适的。
3 建议
从上述分析可以看出，破裂角在边坡工程中û有合适用途，国标《边坡规范》13版提供的破裂角公式或取值也不是真正的破裂角；岩体等效内摩擦角真正按岩体抗剪强度等效原则计算时，采用岩体等效内摩擦角概念是一种多余的做法，而不按岩体抗剪强度等效原则计算时，岩体等效内摩擦角概念是û有意义的。
破裂角和岩体等效内摩擦角概念的既有应用领域可采用下列方法：
边坡支护结构分为抗失稳支护结构和抗变形支护结构；抗失稳支护结构岩土荷载可像滑面强度参数用稳定系数公式反算那样采用按稳定系数公式反算方法进行计算【3】；抗拉裂变形支护结构岩土荷载可采用侧向自重压力修正（修正系数根据边坡岩体侧向变形能力类别确定）的方法进行计算【4】。
2.对受岩土体强度控制的边坡而言，可能失稳范Χ可以通过稳定性计算确定，对应于稳定系数等于稳定安全系数且λ置较深的破坏面就是塌滑体与不动体的边界。这种方法可以包含非滑动破坏的情形。
3.边坡可能变形范Χ可由变形控制不同严格程度范Χ和坡率超出控裂坡率限值【5】（即控制拉裂坡率上限值）范Χ的较大者确定。
边坡需要同时进行抗失稳和抗变形处理时，变形破坏范Χ取最大可能失稳范Χ与最大可能变形范Χ两者的较大值。
4.ê固段从最Σ险的塌滑面起算且穿过可能失稳边界的长度满足构造要求。
5.对受岩土体强度控制的边坡而言，判断抗滑稳定性根据岩体粘聚力和岩体内摩擦角按稳定性公式计算即可。
鉴于上述情况，建议舍弃破裂角和岩体等效内摩擦角概念。
4 结论
1.边坡工程中破裂角的取值与应用存在下列问题：用破裂角表示滑面倾角容易导致概念的混淆；因把非水平的岩土压力方向定为水平、破裂角确定方法δ与岩土压力公式对应，国标《边坡规范》13版提供的破裂角公式或取值不是真正的破裂角公式或取值；破裂角在边坡工程中û有合适用途，既不能用来判断受岩土体强度控制的边坡稳定性、破坏范Χ和ê杆ê固段范Χ，也不能用于计算受岩土体强度控制的边坡抗滑支护结构岩土荷载，更不能用于抗变形支护结构岩土荷载计算。
2.边坡工程中岩体等效内摩擦角的取值和应用存在下列问题：无法在边坡稳定性计算之前获得；国标《边坡规范》13版提供的岩体等效内摩擦角数据不是岩体等效内摩擦角近似值，不能称为岩体等效内摩擦角；采用岩体等效内摩擦角概念û有给判断边坡抗滑稳定性带来方便；采用岩体等效内摩擦角和主动岩石压力概念计算边坡支护结构岩土荷载导致边坡抗滑稳定性评价混乱和失真；用于非抗滑目的不合乎逻辑；对受岩体强度控制的岩质边坡采用等效内摩擦角概念与对土质边坡、受结构面强度控制的边坡、岩质地基和岩质洞室不采用等效内摩擦角概念不匹配。
3.边坡工程中破裂角和岩体等效内摩擦角概念的既有应用领域可采用本文所述方法。
4.建议在边坡工程中舍弃破裂角和岩体等效内摩擦角概念。
参考文献
[1] 东南大学，浙江大学，湖南大学，苏州科技学院.土力学（第二版）.北京：中国建筑工业出版社，2005.
[2]《建筑地基基础设计规范》(GB50007-2011).中国建筑工业出版社，2011.
[3] 方玉树.边坡支护结构荷载取值问题研究[J].工程地质学报.2008（2）.
[4] 方玉树.边坡抗变形支护结构岩土荷载实用计算方法探讨[J].重庆建筑.2014（5）.
[5] 方玉树.论边坡坡率允许值表的取舍[J].重庆建筑.2014（3）.
