摘 要: 等价线性化法是一种可借助振型分解反应谱法计算结构非线性地震峰值响应的实用方法,并且能够在设计中预设结构的损伤位置和损伤程度,是一种值得推广的、并可用于复杂结构性能化抗震设计的工程实用分析方法。在前人研究的基础上,通过迭代计算确定结构的损伤模式,并采用更合理的等价线性化模型,完善了等价线性化法的实施流程,并采用该方法分析了一个平面规则结构与一个空间不规则结构的非线性地震峰值响应。与动力弹塑性分析结果的比较表明,所建议的等价线性化法在预测结构整体和局部构件的非线性地震峰值响应方面均具有较好的精度,且具有计算效率高,适用性强等特点。
关键词: 建筑结构;多自由度体系;等价线性化;非线性地震响应
0 引言
基于经济与损失的均衡,根据现行的建筑结构抗震设防目标,在强烈地震作用下建筑结构的损伤是不可避免的,而建筑结构的诸多抗震性能,如中震下的可维修性和大震下的安全性等,都与其损伤模式与损伤程度直接相关。为此,性能化抗震设计应首先对建筑结构在设计强震作用下的预期损伤位置和损伤程度进行设计,并通过可靠的计算分析予以保证。在这样的设计理念指导下,线弹性结构分析手段已无法胜任,为此,动力弹塑性分析或静力弹塑性分析等更加复杂的结构非线性分析方法日益受到重视。等价线性化法是一种适用于性能化抗震设计、计算结构非线性地震峰值响应的工程实用化方法。该方法通过预设结构损伤模式和预期损伤程度,建立结构的等价线性化模型,如图1所示。图中ζ0为结构的初始阻尼比,为ζe结构的等价阻尼比,K0为构件的初始刚度,Ke为结构的等价刚度。预期损伤的部位或构件在地震作用下可能发生屈服,刚度降低,且在地震反复作用下具有一定弹塑性滞回耗能能力。在等价线性化结构模型中,这些具有非线性力学特性的构件用具有等价刚度的线弹性构件替代,并通过赋予整体结构一个附加等价阻尼比来考虑各损伤部位或构件的滞回耗能对结构整体地震响应的影响。对于等价线性化结构,可以采用振型分解反应谱法来计算结构的非线性峰值地震响应,包括结构整体地震峰值响应,如结构侧移和层间侧移,也包括结构构件的地震峰值响应,如损伤构件或损伤部位的延性系数等。为使假设的损伤模式与损伤程度与计算得到的结构响应相一致,有必要进行少量的迭代。与动力弹塑性分析方法相比,该方法直接利用反应谱进行计算,计算效率高,也可避免因地震动不同所引起的动力弹塑性分析结果差异较大的问题。与静力弹塑性分析相比,该方法具有振型分解反应谱法的优点,可以方便地应用于空间结构,且通过考虑更多振型的参与,也可用于不规则结构,具有更强的适用性,避免了静力弹塑性分析方法的一些局限性,如结构地震响应需以第一振型为主(即使采用MPA方法,一般情况下所用振型数也很少)、不同侧力模式的影响、难以用于高阶振型参与程度较大或振型耦合较大的空间不规则结构等 [1-2] 。
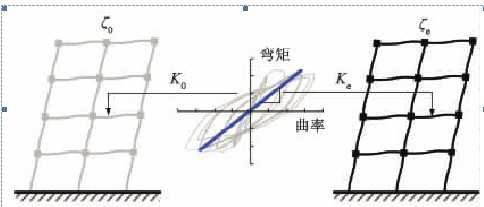
图1 等价线性化法的基本原理
Shibata和Sozen(1976) [3] 首先提出了以多自由度的等价线性化为基础的等代结构法,用于估计地震作用下钢筋混凝土框架结构中非预期损伤构件的承载力需求和预期损伤构件的变形能力需求,但因没有采用迭代计算,假设的损伤模式与实际结果存在差异,这使得早期的等代结构法的完整性存在不足,计算误差较大。尽管如此,他们的工作奠定了等价线性化法的基本构架。在此之后的几十年间,关于多自由度体系的等价线性化法的研究非常少见。直到1994年,Bonacci(1994) [4] 重新审视了等价线性化法在基于位移建筑结构抗震设计中的优势,并通过试验研究验证了Shibata和Sozen(1976) 所提出的单自由度系统等价阻尼比的计算方法的可靠性。在ATC-40 [5] 的第8章中,允许使用基于多自由度体系的等价线性化法作为静力弹塑性方法的补充;日本建筑学会建议的延性保证型设计允许在“屈服机制设计”阶段使用等价线性化方法 [6] 。但ATC-40未给出相关的具体实施方法,而日本建筑学会建议的等价线性化方法近似程度较大。
近年来,随着我国复杂和超限结构的不断出现和性能化设计的推进,国内对超限高层建筑中的关键构件提出了“中震弹性”与“中震不屈服”的性能目标 [7] 。《建筑抗震设计规范》则将其进一步完善,提出了4个等级的性能目标。周颖、吕西林(2008)通过算例研究表明 [7] ,同时提高结构中所有构件的抗震性能目标,将大幅提高结构造价,因此建议区别对待结构中的不同构件,而仅对关键部位和关键构件采用更高的性能目标,这意味着同一水准地震作用下结构中的不同重要性构件可具有不同的损伤程度。直接按弹性分析得到的内力与变形结果,并采用不同的安全储备进行构件设计,虽然能够在一定程度上体现不同构件的不同性能目标,但忽视了构件损伤对结构的刚度等重要动力特性以及构件之间的内力重分布的影响,这可能使得所预期的结构性能与结构实际性能状态有较大误差。等价线性化法可根据不同的性能目标,为结构中不同的构件赋予不同损伤目标,并由此确定相应的等价刚度与等价阻尼,再通过结构整体分析比较准确地确定结构在地震作用下的位移与内力响应,从而为具有不同性能目标的构件的抗震设计提供更加合理的依据。
本文在前人研究的基础上完善等价线性化法的基本流程,并以动力弹塑性分析为依据,采用典型算例验证等价线性化法在计算结构弹塑性地震峰值响应方面的有效性。在进行动力弹塑性分析时,文献[8]采用清华大学开发的基于有限元程序ABAQUS的纤维截面杆系模型对构件的往复加载试验以及钢框架结构、钢筋混凝土框架结构的振动台试验进行了模拟,取得了良好的模拟效果,验证了该模型的有效性。
1 等价线性化法的基本流程
等价线性化法的主要步骤是: ① 建立等价线性化结构; ② 振型分解反应谱分析; ③ 迭代计算确定结构的弹塑性响应,其基本流程如图2所示。尽管采用迭代计算,但由于每次计算分析均采用反应谱分析方法,等价线性化法的计算效率比动力弹塑性分析高很多。
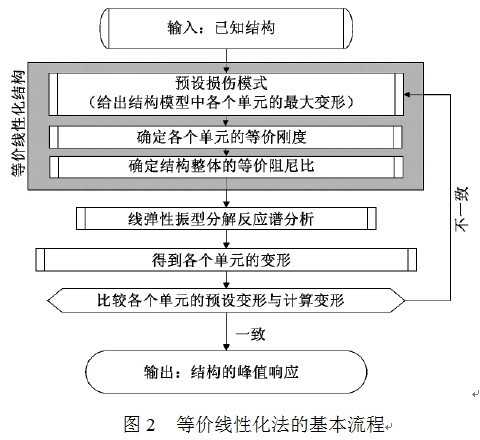
结构损伤模式的确定是等价线性化法在性能化抗震设计中最有价值之处,也是等价线性化法的基础。根据等价线性化分析的目的不同,结构损伤模式的确定分为以下两种情况。
(1) 用于结构抗震性能的复核。此时结构中各个构件的承载力与变形能力均为已知。采用等价线性化法分析时,理论上结构损伤模式可以先任意设置,通过图2所示的迭代计算可使其逐步收敛到结构在设计强震作用下的稳定损伤状态。该迭代过程能够自动考虑结构中各个构件的内力重分布,判断结构的损伤部位并计算相应损伤程度。尽管初设的损伤模式对分析结果影响不大,但合理选择初始的结构损伤模式有助于计算尽快收敛。
(2) 用于结构抗震设计。根据结构中不同构件各自的性能目标,设置不同的初始损伤状态和损伤程度的限值。如对于以“完好”为性能目标的构件,则对应于无损状态,这些构件始终保持其初始刚度,并且不提供滞回耗能;对于允许出现一定程度损伤的构件,则赋予其等价刚度和等价阻尼比,同时可以通过设定延性限值,限定其允许发生的塑性变形的程度。在上述限制条件下,图2所示的等价线性化分析流程可能无法收敛,这意味着当前的结构布置无法实现预设的损伤模式,而需要对结构布置、构件刚度等进行调整,即在图2所示的基本流程的基础上增加调整结构布置的过程,直到等价线性化分析能够收敛到预设的损伤模式。分析一旦能够收敛,则可以得到不同性能目标构件的承载力需求或变形能力需求,如对于要求保持“完好”的构件,可以得到其承载力需求,对于预期损伤构件,可以得到其承载力与变形能力需求。
本文暂时仅讨论上述第(1)种情况的等价线性化法及其应用,第(2)种情况将另文研究。
2 等价线性化法需解决的关键问题
在图2所示的等价线性化法基本流程中,结构构件损伤状态的表达、等价刚度与等价阻尼比的确定,以及不同阻尼比的反应谱等,都是该方法需解决的关键问题,详述如下。
2.1 结构构件的损伤
对于以最大位移为计算目标的等价线性化方法,采用最大塑性变形来定义损伤程度更为合适,如可简单地用构件变形比μ来定义其损伤程度。
对于以弯曲屈服控制的压弯构件
对于以轴向屈服控制的构件
其中, 和 为构件截面的最大曲率和屈服曲率;Δ和Δy为构件的最大轴向变形和屈服轴向变形。
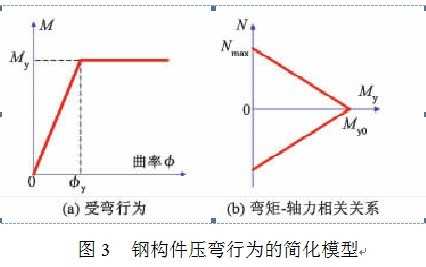
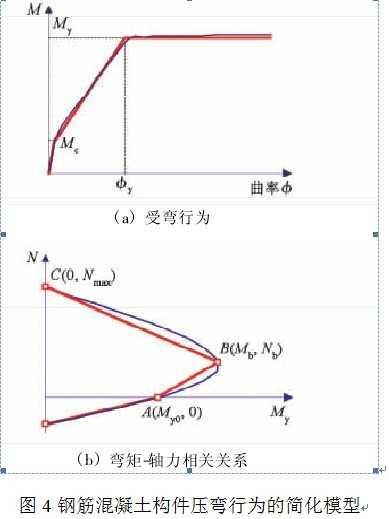
受弯屈服压弯杆件的受力行为可以用弯矩-曲率关系和屈服弯矩-轴力相关关系来表达。对于材料行为比较简单的钢构件,可以将上述关系简化为图3所示的线性关系。其中,My0为截面在纯弯时的屈服弯矩;Nmax为截面可承受的最大轴力。对于钢筋混凝土构件,则可以采用如图4所示的简化模型。其中,截面的开裂弯矩Mc、屈服弯矩My、最大轴力Nmax以及界限破坏对应的弯矩Mb与轴力Nb等都可以通过截面分析得到。同样,对于防屈曲支撑等以轴向屈服控制的构件,其受力行为可以简化为轴力-轴向变形曲线。
2.2 等价刚度与等价阻尼比
为构件预设某一变形比μ,或由等价线性化分析得到构件最大截面曲率 或最大轴向变形Δ并根据构件受力特征由式(1)和图3或图4计算得到某一构件的变形比μ后,则可以按照多种方法计算该构件的等价刚度与等价阻尼比。各国学者提出了许多不同的单自由度等价线性模型,其中比较有代表性的如Gulkan模型 [9] ,Gates模型 [10] ,Iwan模型 [11] ,Kowalsky模型 [12] 等,也有不少学者通过大量的分析对这些方法的精度进行了评价 [13-15] 。总的来说,根据确定等价刚度的方法不同,这些等价线性化方法可以分为两类,即:
(1) 采用最大位移对应的割线刚度为等价刚度,同时采用较大的等价阻尼比;
(2) 采用最大位移对应的割线刚度与初始刚度之间的某个刚度为等价刚度,等价阻尼比小于第(1)类方法。
Iwan等(1979) [13] 指出,上述两类方法在精度方面表现相当。Miranda等(2002) [15] 的研究表明,第(2)类模型中比较有代表性的Iwan模型 [11] 略好于第(1)类模型中有代表性的Kowalsky模型 [12] 。
然而,与单自由度系统等价线性化有所区别的是,结构的等价线性化法分析除了要计算结构的位移响应外,计算结构中各个构件的力的响应也同样重要。第(2)类方法在准确估计位移响应时将高估力的响应,使其在结构等价线性化法应用中会引起较大误差。因此,本文建议采用第(1)类方法。其中,Kowalsky模型 [12] 比较有代表性,该方法给出的等价阻尼比计算公式如下:

点视为一个单自由度系统,应用式(2)和式(3),得到相应的等价刚度和等价阻尼比,再由各高斯点的等价刚度集成得到整个结构的等价刚度矩阵。同样,将高斯点的“等价阻尼比”通过式(4)的能量加权平均的方法转化为整体结构的等价阻尼比
: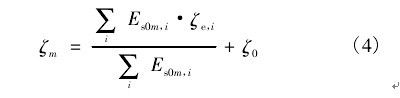
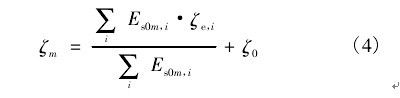
其中,i和m分别是单元号和结构的模态号;ζm为结构第m阶振型的等价阻尼比;Es0m,i为结构发生第m阶振型的变形时,第i个单元的弹性应变能。
2.3 反应谱
等价线性化法的特点之一是能够直接应用反应谱计算结构的地震响应,从而便于与现行抗震规范相衔接。目前各国抗震规范,如我国现行抗震规范 [16] ,日本的建筑基准法 [17] ,以及美国的ASCE 7 [18] 等,均以反应谱的形式给出结构抗震设计所采用的设计地震动,并都引入了一些阻尼修正系数,以在5%阻尼比反应谱的基础上得到不同阻尼比的反应谱。此外,各国学者也提出过多种阻尼比修正系数,比较有代表性的如Shibata和Sozen(1976) [3] ,Newmark和Hall(1982) [19] ,Lin和Chang(2003) [20] 等提出的阻尼比修正系数。但可能因为这类不同阻尼比的反应谱主要应用于消能减震结构的设计,普遍偏于保守,当用于等价线性化方法以确定结构非线性地震峰值响应时,可能引入较大的误差,且随着阻尼比的增大,误差也会增大。这种误差并不是等价线性化法本身的不足。为排除阻尼比修正系数可能引起的误差,验证等价线性化法本身的有效性,本文直接以多条强震记录在不同阻尼比下计算得到的反应谱平均值作为等价线性化法分析时采用的反应谱。从PEER/NGA强震记录数据库中挑选出19条地震波,并将其地面峰值加速度PGA统一调幅至400gal,即对应于我国抗震设计中8度抗震设防的罕遇地震水平。5%阻尼比下的拟加速度反应谱和平均反应谱如图5a所示,不同阻尼比下的平均反应谱如图5b所示。
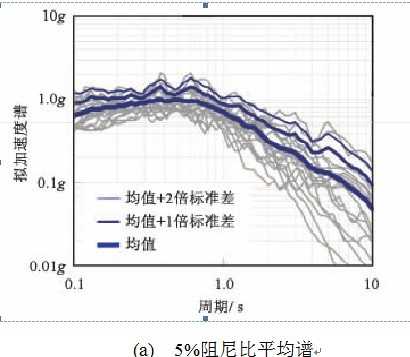
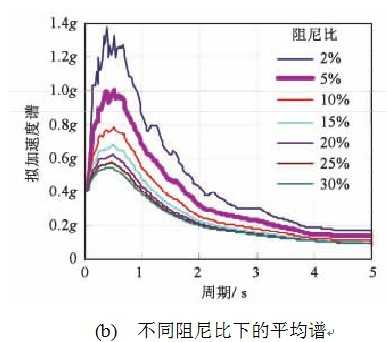
图5分析所采用的平均反应谱至此,图1所示等价线性化法所需的等价刚度Ke、等价阻尼比ζe和对应于不同阻尼比的反应谱等问题已确定。下面,通过两个算例说明等价线性化法在罕遇地震作用下的结构峰值响应分析,并将分析结果与动力弹塑性分析结果进行比较,以验证等价线性化法的准确性。本文以完善并验证等价线性化分析流程为目标,故以下算例暂时仅针对构件力学性能比较简单的杆系钢结构。
3 等价线性化方法在规则结构中应用
图6为一个规则的15层钢支撑框架结构,首层层高5m,其余各层层高均为4m,结构总高度为61m。在沿x方向的各榀框架的中间跨沿结构全高布置防屈曲支撑。从结构中隔离出x方向的中间一榀框架建立分析模型(图6b),模型中各个构件的截面尺寸列于表1。该结构中,支撑部分提供的抗侧刚度约为框架部分的2倍。在地震作用下,防屈曲支撑是预期的损伤耗能构件,使用屈服强度较低的LY100钢材,屈服强度为130MPa;框架柱是关键构件,使用屈服强度较高的HT590钢材,屈服强度为420MPa;框架梁采用Q235B钢材,屈服强度为235MPa。
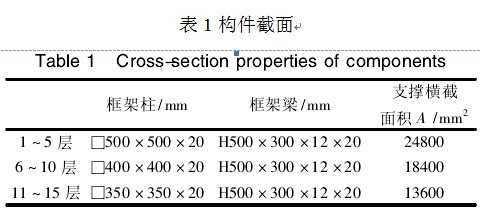
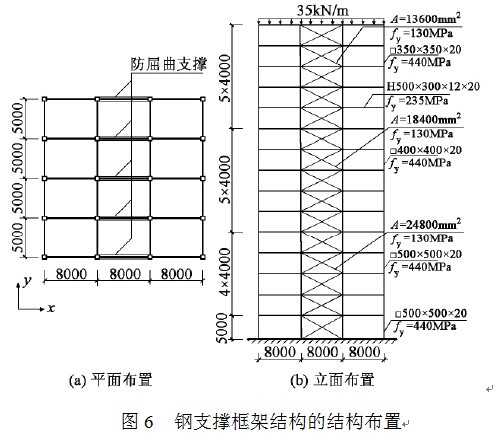
除构件自重外,结构每层梁上均承担35kN/m的附加竖向均布荷载,这些荷载均按质量考虑用以确定地震作用。分别采用等价线性化法(EL-RSA)和动力弹塑性分析(NL-TH)计算结构的地震峰值响应。在动力弹塑性分析中,采用地面峰值加速度PGA调幅至400gal的19条地震输入来计算结构的弹塑性地震响应,而等价线性化法则以图5b的反应谱来计算结构的弹塑性地震响应。动力弹塑性分析采用清华大学开发的基于有限元程序ABAQUS纤维截面杆系单元的本构模型 [8] 。采用ABAQUS中的B23单元建模,其中用于模拟防屈曲支撑的单元两端将弯矩释放,使其只承受轴力作用。有限元模型共包含354个单元,总自由度数为810。分析得到的结构水平位移和层间位移角的对比见图7,构件变形比(即损伤程度)的对比见图8。从图中可以看出,等价线性化法预测的结构的最大位移、最大层间位移角以及构件变形比均与动力弹塑性分析的平均结果非常接近。值得注意的是,如图8所示,等价线性化法能够正确预测结构的损伤模式和损伤程度。该钢支撑框架结构的中柱除在底层柱脚出现屈服外,其余各层均保持在弹性范围内;下部楼层的钢支撑则基本屈服,且在抗侧刚度发生变化的楼层,钢支撑的屈服程度较相邻楼层更大。
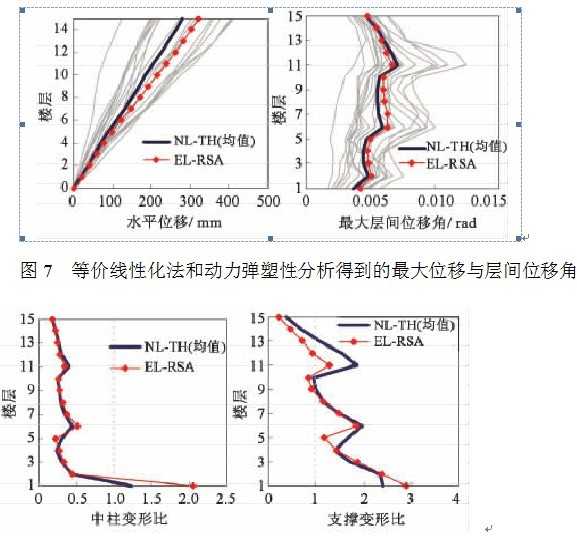
图8 等价线性化法和动力弹塑性分析得到的构件变形比
表2结构构件的属性

4 等价线性化法在空间不规则结构中的应用
以图9所示的复杂空间钢支撑框架结构为例,说明等价线性化法在空间不规则结构中的适用性。该结构是由两个倾斜塔楼和一个巨大悬臂组成,共12层,外周边框架上布置了巨型斜撑以增加其抗侧和抗扭刚度,如图10所示。此外,还在某些楼层设置了水平支撑以进一步提高结构的抗扭刚度。各个构件的材料属性和截面参数见表2。
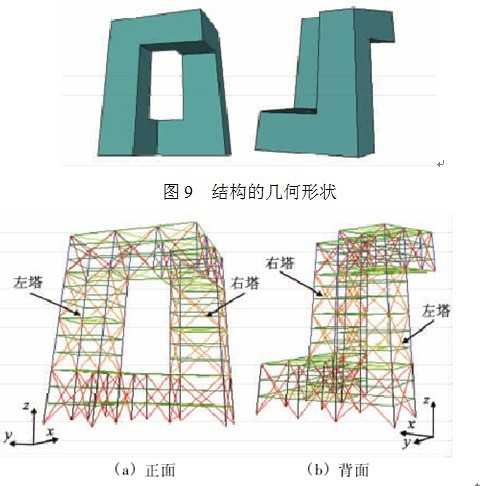
图10结构布置
除构件自重外,各梁(不包括水平斜撑)均承受25kN/m的附加竖向均布荷载,这些荷载均按质量考虑用以确定地震作用。表3给出了结构的模态信息。可见在地震输入的x方向上,不但高阶振型参与很大,而且前两阶振型的周期接近、振型参与质量均较大,振型耦合程度大。
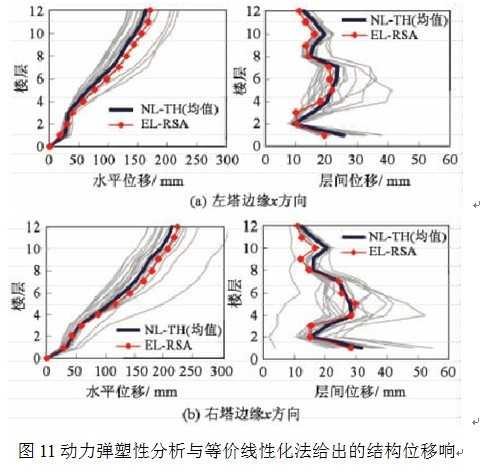
等价线性化法采用前10阶模态参与反应谱分析,并采用CQC法进行振型组合。动力弹塑性分析和等价线性化法分析均只在结构的x方向输入单方向的地震作用。动力弹塑性分析采用与上节算例相同的方法和建模方式。图11比较了两种方法得到的结构两个关键竖向轴线位置的峰值位移响应,图中的位移是两个水平方向位移分量的组合,可见两种分析方法的结果吻合良好。
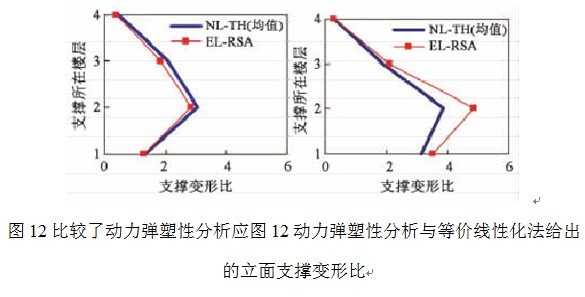
同样,等价线性化法比较准确地把握了结构的损伤模式和损伤程度。该结构的损伤主要集中在沿x方向的立面支撑上。与等价线性化法计算得到的x方向立面支撑的变形比,可见等价线性化法在统计意义上与动力弹塑性分析结果吻合良好。

5 结语
本文在前人研究的基础上,建立了采用等价线性化法计算建筑结构地震峰值响应的完整流程。通过对规则结构与不规则结构的分析计算表明,对于在地震作用下具有稳定损伤模式的结构,等价线性化法给出的结构位移、构件变形和结构损伤模式等预测结果均与动力弹塑性分析结果在统计意义上吻合良好。与动力弹塑性分析相比,等价线性化法在以下方面具有优势:
(1) 等价线性化法可以直接应用设计反应谱计算结构的非线性地震峰值响应,这为评价建筑物的抗震性能提供了统一的依据,与少数地震动记录输入下的动力弹塑性分析相比,可避免因地震动记录选取的不同而带来的不确定性。同时,等价线性化法的计算效率高,通常仅需几次弹性反应谱分析的迭代计算即可。
(2) 等价线性化法可以体现结构损伤模式和不同构件的损伤程度对结构动力特性和内力分布的影响,便于实现建筑性能化抗震设计目标。
但另一方面,等价线性化法以反应谱分析为基础,不可避免的继承了反应谱分析的局限性,如难以考虑地震过程中结构构件的低周疲劳特性对结构抗震性能的影响。因此,不建议将等价线性化法用于巨震作用下损伤非常严重甚至接近倒塌状态的结构地震响应分析。同时,使用等价线性化法时,分析对象应该具有比较稳定的损伤模式,计算才能收敛。这一要求实际上也是结构抗震性能设计的重要目标,即在预期强烈地震下,无稳定损伤模式的结构,其抗震性能必然不好。
为了将等价线性化分析用于工程抗震设计,还需要在以下方面进一步开展深入的研究工作:
(1) 我国现行抗震规范中对应于较高阻尼比的设计反应谱过于保守,不适宜直接用于等价线性化法。应根据我国建筑性能化抗震设计的要求,对用于等价线性化法的设计反应谱进行必要的研究。
(2) 除了本文介绍的杆系钢结构之外,等价线性化分析在钢筋混凝土结构(框架、框架-剪力墙和剪力墙结构)以及消能减震结构中的应用及对其准确性的检验仍需开展进一步工作。
(3) 单自由度等价线性化模型是等价线性化分析的基础。文中采用的Kowalsky模型是根据Taketa滞回模型得到的,可能不适用于具有其他滞回特性的结构构件的等价线性化分析,因此有必要深入地讨论滞回模型对等价线性化的影响,并建立能够考虑不同滞回模型影响的单自由度等价线性化模型。
参考文献:
[1]Krawinkler H,Seneviratna G D P K.Pros and cons ofa pushover analysis of seismic performance evaluation[J].Engineering Structures,1998,20(4-6):452-






